Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.Problemas - Ex. 54
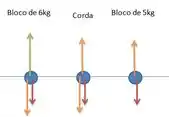
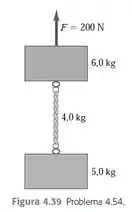
Os dois blocos indicados na figura estão ligados por uma corda uniforme e pesada, com massa . Uma força de é aplicada de baixo para cima conforme indicado.
- Desenhe três diagramas do corpo livre, um para o bloco de , um para a corda de e outro para o bloco de . Para cada força, indique qual é o corpo que exerce a referida força.
- Qual é a aceleração do sistema?
-
Qual é a tensão no topo da pesada corda? - Qual é a tensão no meio da corda?
Passo 1
Antes de tudo, é importante notar que nesse exercício a massa da corda foi fornecida e ela não pode ser desprezada, como nos outros exercícios. Aqui precisamos levar ela em consideração!
Nesse sistema agem três forças: a força tensora, a força peso e a força que é aplicada apenas em um dos blocos. O problema pede para cada componente desse sistema, um diagrama do corpo livre, mas para isso precisamos identificar em cada um deles as forças.
No bloco de : como ele está bem em cima do sistema, a força é apenas aplicada nele, vertical para cima com módulo de . Para baixo temos o peso (força com que a Terra puxa esse bloco para baixo) e também para baixo temos a tensão da corda. A tensão da corda é referente ao topo da corda! Ou seja, levando em conta toda extensão da corda.
No bloco de : temos apenas duas forças: a força peso (exercida pela Terra sobre esse bloco) vertical para baixo e a força tensora. Nesse caso a força tensora é referente à base da corda e é vertical para cima, é uma força de sustentação do bloco.
Por último temos a corda: na corda, como a massa dela não é desprezível, temos a força peso agindo sobre ela. Temos também a força de tensão na parte superior (vertical para cima) e na parte inferior (vertical para baixo).
O diagrama de corpo livre fica assim ó:
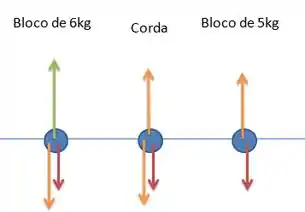
Em verde está represnetada a força , em vermelho estão representadas as forças peso em cada um dos componentes do sistema e em laranja estão as forças tensoras. Se nós colocarmos “em ordem” vamos ver que as forças tensoras serão canceladas, pois elas configuram o que chamamos de “forças internas” e elas só aarecem no sistema quando isolamos um pedaço dele, seja só um bloco, ou um pedaço da corda, etc..
Olha só como esses diagramas ficariam “empilhados”:
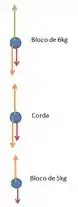
Passo 2
Para determinar a aceleração do sistema, devemos olhar para o todo! Feito isso as unidas forças que realmente contribuem são os pesos (de cada bloco e da corda) e a força externa de . Aplicando a segunda lei temos:
Como o movimento é todo na vertical, podemos esquecer essa equação vetorial e apenas ficar com a parte em :
Passo 3
Para determinar a tensão no topo da corda, como já sabemos a aceleração, vamos usar o diagrama de corpo livre do bloco superior de . Como mencionado no passo há três forças agindo sobre ele: a força peso, a força extrena e a força de tensão da parte superior da corda, e é exatamente essa última que estamos interessados!
Aplicando a segunda lei nesse bloco temos:
Passo 4
No meio da corda estão agindo o peso (referente a metade da massa da corda), a tensão na parte superior (que calculamos no passo anterior) e a tensão no meio, que é o que queremos. A aceleração a que essa corda está submetida é e a massa dela é . Aplicando a segunda lei temos:
Resposta
