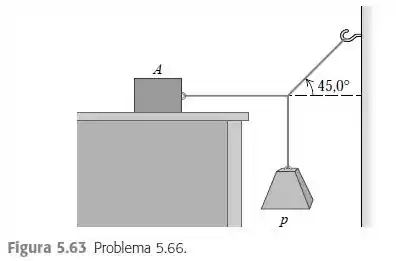
- O bloco A da Figura 5.63 pesa 60,0 N. O coeficiente de atrito estático entre o bloco e a superfície sobre a qual ele se apóia é de 0,25. O peso p é igual a 12,0 N, e o sistema está em equilíbrio. Calcule a força de atrito exercida sobre o bloco A. b) Ache o peso p máximo que permite ao sistema ficar em equilíbrio.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte sistema:
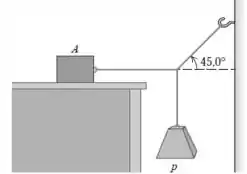
Queremos calcular a força de atrito exercida sobre o bloco dado que:
- O sistema está em equilíbrio (a aceleração é zero);
- O peso p é igual a ;
- O bloco A da pesa ;
- O coeficiente de atrito estático entre o bloco e a superfície sobre a qual ele se apóia é de .
Também devemos encontrar o peso p máximo que permite ao sistema ficar em equilíbrio.
Para resolver isso, temos que fazer um diagrama de corpo livre do sistema e analisar as forças que estão atuando no corpo.
Também, utilizaremos também a segunda Lei de Newton:
Onde é a força resultante, é a massa e é a aceleração.
Passo 2
- Vamos desenhar o diagrama de corpo livre para o peso suspenso:
- Temos todos os mesmos diagramas de corpo livre e equações de força da parte (a), mas agora a força de atrito estático tem seu maior valor possível,
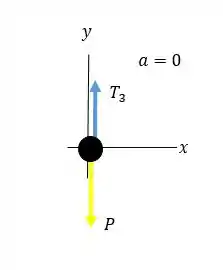
E então, vamos aplicar a segunda lei de Newton no peso. Nós só temos forças na vertical, então:
Lembrando que a aceleração é nula. Então:
Onde é a força peso e é a tensão na corda.
Passo 3
Agora vamos desenhar um diagrama de corpo livre para o nó:
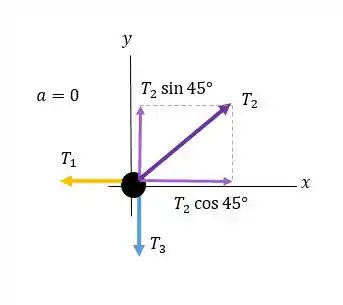
E então, vamos aplicar a segunda lei de Newton no nó. Nós temos forças na horizontal e na vertical então vamos aplicar as leis de Newton para ambos:
No :
Passo 4
No :
Passo 5
E então, vamos esboçar o diagrama de corpo livre sobre o bloco, e aplicar a segunda lei de Newton nele:
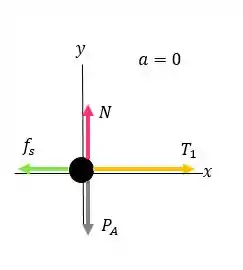
Para descobrirmos os atrito, vamos aplica-la no :
Passo 6
Onde é o coeficiente de atrito é a força de atrito e é a força normal.
Então ,
Passo 3
Das equações da força do nó:
Passo 4
E então podemos encontrar :
Passo 5
E por fim, podemos encontrar o peso P: