Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.Problemas - Ex. 65

Dois discos metálicos, um com raio R 1 =   2,50   c m   e massa M 1 =   0,80   k g e outro com raio R 2 =   5,0   c m e massa M 2 =   1,60   k g , são unidos por uma solda e montados sobre um eixo sem atrito passando no centro comum dos discos, como no Problema 9.89. a) Um fio leve é enrolado em torno da periferia do disco menor, e um bloco de 1,50   k g é suspenso na extremidade livre do fio. Qual é o módulo da aceleração de cima para baixo do bloco depois que ele é libertado?

b) Repita os cálculos da parte (a), agora supondo que o fio seja enrolado na periferia do disco maior. Em qual dos dois casos a aceleração é maior? Sua resposta faz sentido?

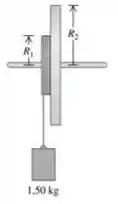
Passo 1

Eaee, belezinha??? Bom... o enunciado nos diz que dois discos metálicos, um com raio R 1 =   2,50   c m   e massa M 1 =   0,80   k g e outro com raio R 2 =   5,0   c m e massa M 2 =   1,60   k g , são unidos por uma solda e montados sobre um eixo sem atrito passando no centro comum dos discos:

Queremos encontrar o módulo da aceleração de cima para baixo do bloco depois que o bloco é libertado.

Como dado, o enunciado nos diz que um fio leve é enrolado em torno da periferia do disco menor e o bloco de 1,50   k g é suspenso na extremidade livre do fio.

Também queremos fazer a mesma coisa com o disco maior.

Para resolver isso, precisaremos das seguintes expressões:

F → = m a

∑ �� = I α

Onde F é força, m é massa, a é aceleração, τ é torque, I é momento angular e α é aceleração angular.

Passo 2

Letra a)

Aplicaremos F → = m a para o bloco e ∑ τ = I α para a sua movimentação. O momento de inércia do discos é dado por I = 1 2 M R 2 ,

I d i s c o s = 1 2 ( 0,80   k g ) 0,025   m 2 +   1 2 ( 1,60   k g ) ( 0,05   m ) 2

I d i s c o s = 0,00225   o u   2,25 × 10 - 3

Para encontrar a tensão na corda T , precisamos aplicar uma relação de forças peso e tensão, igualando à F → = m a .

Assim, poderemos encontrar a aceleração. Vamos para os cálculos.

Passo 3

Fazendo a relação entre as forças, teremos

m g - T = m a

Como, T R = I α = I a R , logo T = I a R 2

m g - I a R 2 = m a

m g = m a + I a R 2

Colocando a em evidência...

m g = a ( m + I R 2 )

a = m g m + I R 2 ou a = g 1 + I m R 2

Para m = 1,50   k g e R = 0,0225   m ,

a = 9,8   m / s 2 1 + 0,00225 ( 1,50   k g ) ( 0,025   m ) 2

a = 2,88   m / s 2

Passo 4

Letra b)

Supondo que o fio seja enrolado na periferia do disco maior, temos m = 1,50   k g e R = 0,05   m

a = 9,8   m / s 2 1 + 0,00225 ( 1,50   k g ) ( 0,05   m ) 2

a = 6,13   m / s 2  

Teremos, portanto, uma aceleração maior.

Sendo assim, com a corda presa ao disco maior, a tensão na corda é capaz de aplicar um torque maior.

Resposta

a) a = 2,88   m / s 2

b) a = 6,13   m / s 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O motor de um carrossel exerce um torque constante sobre ele. Saindo do repouso e ganhando rapidez, a potência desenvolvida pelo motor (a) é constante, (b) Cresce linearmente com a rapidez angular do
Um torque resultante constante atua sobre um carrossel desde a partida, até que ele atinja a rapidez de operação. Durante este tempo, a energia cinética do carrossel (a) é constante, (b) cresce linear
A orientação da velocidade angular de um corpo é, necessariamente, a mesma do torque resultante sobre ele? Explique. Se o torque resultante e a velocidade angular têm sentidos opostos, o que isto lhe
Uma forma de identificar se um ovo está cozido ou não sem quebrá-lo, é colocar o ovo sobre uma superfície horizontal rígida e tentar girá-lo. Um ovo cozido vai girar com facilidade, contrariamente ao
Verdadeiro ou falso: Se o torque resultante sobre um objeto em rotação é zero, a velocidade angular do objeto não pode mudar. Se sua resposta é “falso”, dê um exemplo de tal situação.