Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 51
Dois blocos ligados por um cordão (figura abaixo) deslizam para baixo sobre um plano inclinado de . O bloco 1 tem a massa = 0,80 kg e o bloco 2 tem a massa = 0,25 kg. Ademais, os coeficientes de atrito cinético entre os blocos e o plano são 0,30, para o bloco 1 e 0,20 para o bloco 2. Encontre (a) a magnitude da aceleração dos blocos e (b) a tensão no cordão.
Passo 1
Letra (a)
A gente quer a magnetude da aceleração dos blocos. Então a gente pode pensar em usar a segunda lei de Newton neles:
E para isso a gente precisa dos diagramas de corpo livre desses dois carinhas:
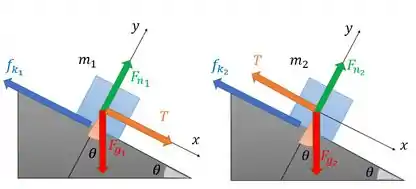
Temos a tensão onde temos cordinha, temos força peso para baixo nos dois casos, e também a força normal porque há contato entre bloco e superfície. E temos a força de atrito cinético contrária ao movimento.
Como esses blocos estão somente sob ação da gravidade como força externa, então eles devem estar descendo a rampa, assim a força de atrito aponta para o subir da rampa, no sentido contrário ao movimento.
Os dois blocos vão descer com a mesma aceleração porque estão ligados por um mesmo fio tensionado (esticado).
Bora lá achar esse !
Passo 2
A segunda lei de Newton para o bloco no eixo fica:
Sendo que é a a magnitude da aceleração dos blocos. Nessa direção temos a tensão no sentido de positivo, temos a componente de que vai valer , e vai entrar no somatório positiva. Como :
E temos também a força de atrito cinético nessa direção. Ela tem a expressão , como aponta para negativo, ela fica com sinal de menos. Então o somatório em fica:
Já para o eixo vamos ter que porque não há movimento nessa direção. Nela temos e , que vai entrar negativa no somatório pois aponta para negativo:
Substitui (2) em (1):
Passo 3
Agora vamos fazer a mesma coisa, só que no bloco 2.
As equações de e ficam quase iguais. A diferença é que a massa agora é (vamos mudar isso e os demais índices de para 2) e a tensão está no sentido inverso de , ficando negativa na equação da segunda lei de Newton desse eixo.
Para o eixo então vamos ter
E para o eixo a equação fica igual a do outro bloco, só mudamos os índices:
Substitui (5) em (4):
Passo 4
A gente ainda não quer a tensão (isso fica para a letra b), só a aceleração. E temos essas duas equações a partir de cada bloco:
Então podemos sumir com a tração T somando (3) com (6):
Agora isola o :
Passo 5
Agora a gente substitui os valores:
Para saber a magnitude a gente tira o módulo:
Essa aceleração negativa diz que os blocos estão perdendo velocidade enquanto deslizam.
Passo 6
Letra (b)
Como a gente tem o valor de , podemos substituir em uma das equações que a gente tem para achar . Vamos usar (3):
Substituindo os valores, lembrando de usar que foi o que a gente tirou diretamente do sistema:
Resposta
Letra (a):
Letra (b):