Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 47
Um bloco de é projetado rampa acima, com uma rapidez inicial de . O coeficiente de atrito cinético entre a rampa e o bloco é , (a) Se a rampa está inclinada de ° em relação à horizontal, qual é a distância que o bloco percorre sobre a rampa até parar? (b) O bloco volta, então, rampa abaixo. Qual é o menor coeficiente de atrito estático, entre o bloco e a rampa, capaz de evitar que o bloco escorregue de volta?
Passo 1
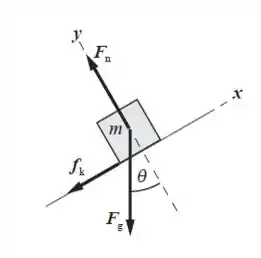
O diagrama abaixo mostra as forças que atuam sobre o bloco quando ele desliza sobre a rampa. Note que o bloco é acelerado por (força de atrito cinético) e o componente x de . Nós podemos usar a equação de Torricelli para expressar o deslocamento do bloco pela rampa como função de sua aceleração e usar a Segunda lei de Newton para encontrar a aceleração do bloco à medida que desliza pela rampa.
Passo 2
Item (a)
Usando a equação de Torricelli, temos:
Como a velocidade final , então:
De acordo com a 2° Lei de Newton no eixo x:
E a 2° Lei de Newton em y, como a soma das forças em y é igual a zero, pois o bloco não sobe nem desce na rampa no eixo y, então:
Passo 3
Substituindo e na equação das somas das forças em x, temos:
E substituindo no somatório das forças em y e multiplicando toda a equação por :
Somando as duas equações acima:
Substituindo no resultado da equação de Torricelli:
Substituindo por valores numéricos:
Passo 4
Item (b)
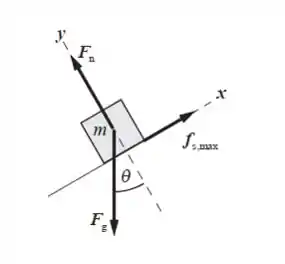
No ponto em que o bloco está instantaneamente em repouso, atrito estático torna-se operativa e, se o coeficiente de atrito estático é muito alto, o bloco não retomará o movimento, mas permanecerá nesse ponto. Podemos determinar o máximo possível
valor de para o qual o bloco ainda desliza para baixo considerando a inclinação e a igualdade da força de atrito estática e o componente do peso do bloco para baixo.
Passo 5
Usando a 2° Lei de Newton no eixo x:
E no eixo y:
Como
Substituindo o valor de :