Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 46

Uma tartaruga de 12   k g está no caminhão do cuidador do zoológico, que percorre uma estrada do interior a 53   m i / h . O funcionário vê um cervo na estrada e freia para parar em 12   s . Supondo a aceleração constante, qual é o menor coeficiente de atrito estático necessário entre a tartaruga e o piso do caminhão para que ela não escorregue?

Passo 1

Podemos determinar a aceleração necessária para o caminhão e tartaruga, considerando o deslocamento de ambos durante determinado intervalo de tempo. O atrito estático deve fornecer uma determinada aceleração para a tartaruga. A tartaruga, se não escorregar, deve ter essa aceleração que é produzida pela força de atrito estático agindo sobre ela.

Usando a definição de força de atrito estática:

f s = μ s F n

Abaixo está representado o diagrama do corpo livre da tartaruga:

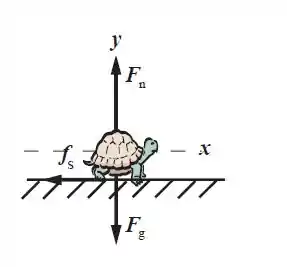
Passo 2

Usando a 2° Lei de Newton no eixo x:

∑ F x =   - f s = m a x

E, como a tartaruga não sobe nem desce:

∑ F y = F n - F g = 0 ⇒ F n = F g = m g

Então, usando a definição de força de atrito estática:

μ s = f s F n = - m a x m g = - a x g

Passo 3

Usando a definição de aceleração:

a x = Δ v Δ t = v f , x - v i , x Δ t

Como a velocidade final é zero, v f , x = 0 ,   então:

μ s = v i , x g Δ t

Substituindo os valores numéricos:

μ s = 55 m i h × 1609 m m i × 1 h 3600 s 9,81 m s 2 12   s = 0,21

Resposta

μ s = 0,21

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é a velocidade terminal de uma bola esférica de 6,00k g que possui um raio de 3,00c m e um coeficiente de arrasto de 1,60 ? A massa específica do ar no local onde a bola está caindo é 1,20k g / m
Calcule o módulo da força de arrasto a que está sujeito um míssil de 53c m de diâmetro voando a 250m / s em baixa altitude. Suponha que a massa específica do ar é 1,2k g / m 3 e o coeficiente de arras
Uma pequena partícula de poluição se aproxima da Terra, flutuando em ar parado. A rapidez terminal da partícula é 0,30m m / s , a massa da partícula é 1,0.10 - 10g e a força de arrasto da partícula é
Uma demonstração típica de sala de aula envolve soltar filtros de café em forma de cesta e medir o tempo que levam para cair por certa distância. Um professor solta um único filtro de café em forme de
Uma bola de ping-pong tem uma massa de 2,3g e uma rapidez terminal de 9,0m / s . A força de arraste é da forma b v 2 . Qual é o valor de b ?