Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 16.Exercícios e Problemas - Ex. 19

Dois dipolos elétricos de módulo p estão afastados um do outro à distância r . A Figura 16.10 mostra cinco possibilidades para as orientações do par de dipolos. Calcule a energia potencial para cada uma das configurações.

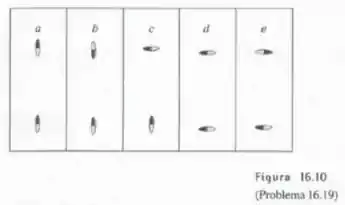
Passo 1

Para calcular a energia potencial de cada configuração, vamos seguir o seguinte procedimento: primeiro achamos o campo produzido pelo dipolo de cima sobre o dipolo de baixo e, daí, usamos a expressão

U = - p → b a i x o ⋅ E → c i m a

Vamos adotar que o lado escuro do dipolo representa a carga positiva e o lado branco a carga negativa. A seguir representamos em vermelho o campo elétrico produzido pelo dipolo de cima e em azul o vetor momento de dipolo elétrico do dipolo de baixo:

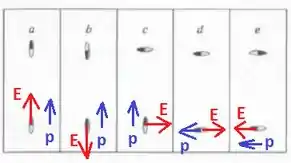
Com isso, vamos ter

U a = - p E z

U b = + p E z

U c = 0

U d = + p E x

U e = - p E x

Passo 2

Nós sabemos que o campo no eixo do dipolo é

E z = p 2 π ϵ 0 r 2

Já na direção perpendicular ao dipolo:

E x = p 4 π ϵ 0 r 2

Essa expressão na direção perpendicular ao dipolo foi calculada no exercício 16.14.

Com isso,

U a = - p 2 2 π ϵ 0 r 2

U b = + p 2 2 π ϵ 0 r 2

U c = 0

U d = + p 2 4 π ϵ 0 r 2

U e = - p 2 4 π ϵ 0 r 2

Resposta

U a = - p 2 2 π ϵ 0 r 2

U b = + p 2 2 π ϵ 0 r 2

U c = 0

U d = + p 2 4 π ϵ 0 r 2

U e = - p 2 4 π ϵ 0 r 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A luz do Sol permite que uma célula solar transfira elétrons do terminal positivo para o negativo realizando 2,4 ⋅ 10 - 19 J de trabalho por elétron. Qual é a fem dessa célula solar?
Qual é a fem de uma bateria que realiza 0,60 J de trabalho para transferir 0,050 C de carga do terminal negativo para o positivo?
Na forma de decaimento radioativo conhecida como decaimento alfa, um núcleo instável emite um núcleo de átomo de hélio, chamado de partícula alfa. Uma partícula alfa contém dois prótons e dois nêutron
O Sol funciona pelo processo de fusão, em que quatro prótons se fundem para formar um núcleo de hélio (dois dos prótons envolvidos se transformam em nêutrons), liberando no processo uma grande quantid
Um dipolo elétrico consiste de duas esferas de 1.0g, carregadas com ± 2.0n C , fixadas às extremidades de um bastão com 10cm de comprimento e de massa desprezível. O dipolo gira praticamente sem atrit