Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 17.Exercícios e Problemas - Ex. 11
No sistema de capacitores em série visto na Figura 17.12, o bloco do centro pode ser deslocado na vertical. Mostre que a capacitância equivalente do sistema independe da posição daquele bloco e calcule .
Passo 1
Sem considerar o bloco no centro, temos uma carga na placa superior e uma carga na placa inferior (representadas em vermelho). Quando colocamos o bloco no centro, termos uma carga induzida na parte superior do bloco e na parte inferior (representada em azul):
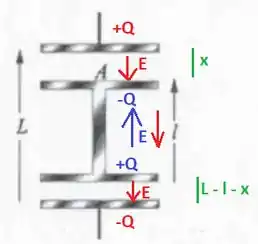
Vou supor que a distância da parte superior do bloco à placa superior é e a distância entre as partes inferior é . Observe que entre as placas do bloco o campo elétrico será nulo pois os campos em azul e em vermelho vão se cancelar!
Lembre-se que
Passo 2
Vamos calcular a diferença de potencial entre as placas, que será basicamente o produto dos campos uniformes pelas distâncias:
Note que a contribuição do campo em azul cancela a contribuição do campo em vermelho na região do bloco!
Substituindo a expressão para :
Como , temos
Por fim, como a capacitância é definida por , segue que
Vemos que essa capacitância independe de , de modo que não importa a posição em que posicionamos o bloco.