Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.Problemas - Ex. 89

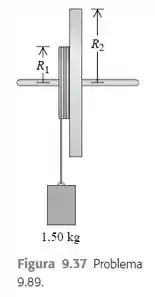
Dois discos metálicos, um com raio R 1 = 2,50 c m e massa M 1 = 0,80 k g e o outro com raio R 2 = 5,0 c m e massa M 2 = 1,60 k g , são soldados juntos e montados em um eixo sem atrito passando pelo centro comum (Figura 9.37). a) Qual é o momento de inércia dos dois discos? b) Um fio fino é enrolado na periferia do disco menor, e um bloco de 1,50   k g é suspenso pela extremidade livre do fio. Se o bloco é libertado do repouso a uma distância de 2,0   m acima do solo, qual é sua velocidade no momento em que atinge o solo? c) Repita o cálculo do item (b), desta vez com o fio enrolado na borda do disco maior. Em qual caso a velocidade escalar final do bloco é maior? Explique por quê.

Passo 1

Oi, galerinha! Tudo bom?

Para calcular o momento de inércia do conjunto, devemos calcular separadamente cada momento de inércia e somá-los. O momento de inércia de um disco girando a partir do seu eixo de simetria é dado por

I = M R 2

Assim sabemos como calcular o momento de inércia do conjunto temos que

I = I 1 + I 2

I = M 1 R 1 2 + M 2 R 2 2

Veja só!

Passo 2

Substituindo os valores, temos que

I = 0,8   k g 0,025   m 2 + 1,6   k g 0,050   m 2

I = 2.25 × 10 - 3 k g . m 2

Tranquilo até aqui?

Passo 3

Para calcular a velocidade com que a Massa presa na extremidade de um dos discos cai, devemos usar o princípio da conservação de energia, onde partindo do repouso, a massa cai enquanto os discos são colocados a girar.

U b i = U b f + K b f + K d

onde U b e K b são as energias potencial e cinética do bloco, respectivamente. Além disso temos K d como a energia cinética de rotação dos discos que giram com uma velocidade ω

Podemos então escrever nossa energias da seguinte maneira:

U b f – U b i = m g d = m v 2 2 + I ω 2 2 = K b f + K d

Lembrando que O bloco e o disco estão ligados, existe um vínculo ligado a velocidade de ambos. Desta forma, temos que

ω = v R 1

Substituindo ω = v R 1 em,

m g d = m v 2 2 + I v 2 2 R 1 2

Resolvendo...

1,5 9,8 2,0 = 1,5 v 2 2 + 2,25 v 2 2 0,025 2

29,4 = 0,75 v 2 + 1800 v 2

v 2 = 29,4 1800,75

Logo a velocidade do bloco ao chegar ao solo será de

v = 0,127 m / s

Bacana, não é?

Passo 4

Repetindo o cálculo para o disco maior, nesse caso o raio utilizado em v = ω R , será o raio do disco 2 R 2 , portanto:

m g d = m v 2 2 + I v 2 2 R 1 2

Resolvendo...

1,5 9,8 2,0 = 1,5 v 2 2 + 2,25 v 2 2 0,05 2

29,4 = 0,75 v 2 + 450 v 2

v 2 = 29,4 450,75

Logo a velocidade do bloco ao chegar ao solo será de

v = 0,065 m / s

E aí! Entendeu tudo? Responde Aí!

Resposta

  1. I = 2.25 × 10 - 3 k g . m 2
  2. v = 0,127 m / s
  3. v = 0,065 m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula se move com uma rapidez constante de 25m / s em um círculo de 90m de raio. (a) Qual é a sua rapidez angular em radianos por segundo em relação ao centro do círculo? (b) Quantas voltas el
Uma bicicleta de 14k g tem rodas de 1,2m de diâmetro, cada uma com uma massa de 3,0k g . A massa do ciclista é 38k g . Estime a fração da energia total do sistema ciclista-bicicleta que está associada
Um disco de 12 cm de raio, que começa a girar em torno de seu eixo em t = 0 , gira com uma aceleração angular constante de 8,0r a d / s 2 . Em t = 5,0s , (a) qual é a rapidez angular do disco e (b) qu
Uma mesa giratória, girando a 33 r e v / m i n , é levada ao repouso em 26 s. Supondo constante a aceleração angular, encontre (a) a aceleração angular. Durante esses 26s , determine (b) a rapidez ang
Considere o pulsar do Caranguejo, discutido na Seção 9-2. Justifique a afirmativa de que a perda de energia rotacional é equivalente à potência emitida por 100000 estrelas. A potência total irradiada