Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.Problemas - Ex. 92
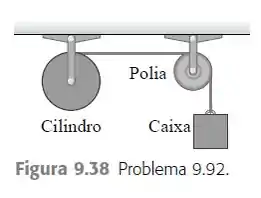
Na Figura 9.38, o cilindro e a polia giram sem atrito em torno de um eixo horizontal fixo que passa pelos seus centros. Uma corda leve é enrolada em volta do cilindro, passa sobre a polia e possui uma caixa de 3,0 kg suspensa por sua extremidade livre. Não há deslizamento entre a corda e a superfície da polia. O cilindro uniforme possui massa de 5,0 kg e raio de 40,0 cm. A polia é um disco uniforme com massa de 2,0 kg e raio de 20,0 cm. A caixa é libertada do repouso e cai à medida que a corda se desenrola do cilindro. Ache a velocidade escalar da caixa após ela ter caído 1,50 m.
Passo 1
Primeiro passo é analisar todas as energias envolvidas no exercício.
Assumindo que o sistema parte do repouso e que nosso sistema de coordenada no eixo da caixa, implicando que, a energia inicial do sistema é nula, ou seja,
Desta forma só nos sobra analisar a Energias Finais do problema.
Passo 2
Temos que a Energia Final do Sistema será
Tanto o cilindro quanto a polia e a caixa estão ligadas pelo movimento de uma corda. Isso implica que as velocidade esão ligadas de forma que
Desta forma temos que as velocidade lineares de cada objeto será a mesma. Podemos escrever a somatória das energias como
Assim teremos
Por fim dizemos que