Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.12 - Ex. 77
Uma bobina retangular com espiras compactas é colocada nas proximidades de um fio retilíneo longo, como mostra a figura 30-66. Qual é a indutância mútua da combinação fio-bobina para ?
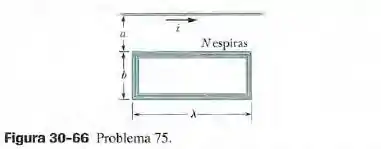
Passo 1
O fluxo magnético através da espira do campo produzido pela corrente é dado por:
Passo 2
A força eletromotriz produzida em uma das bobinas é proporcional à taxa de variação da corrente na outra. As constantes de proporcionalidade e são iguais, o que nos permite simplificar um pouco a escrita: .
O enlaçamento do fluxo é dado por:
Substituindo os valores na expressão acima, temos:
Resposta
A indutância mútua dos solenoide é:
Exercícios de Livros Relacionados
28- Um solenoide fino possui 900 espiras por metro e raio igual a 2.50c m . A corrente no solenoide cresce com uma taxa uniforme de 60.0A / s . Qual é o módulo do campo elétrico induzido em um ponto p
30- O campo magnético B → em todos os pontos do círculo no interior do anel indicado na Figura 29.31 possui um módulo inicial igual a 0.750T . (O círculo poderia representar aproximadamente o espaço n
43- Considere dois solenoides, um dentro do outro. O solenoide externo possui comprimento de 50.0c m e contém 6750e s p i r a s , enquanto o solenoide coaxial interno tem 3.0c m de comprimento e 0.120
Um fio metálico isolado, de resistividade ρ e seção transversal de área S , é enrolado num cilindro de raio a e comprimento l , ficando com N espiras bem juntas uma das outras. As extremidades do fio
Uma espira circular de raio a , auto-indutância L e resistência R gira em torno do eixo z , com velocidade angular constante ω , num campo magnético uniforme B → .a) Calcule a fem E e a corrente I ind