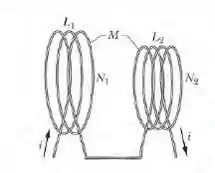
As duas bobinas da figura 30-72 têm indutâncias e quando estão muito afastadas. A indutância mútua é . (a) Mostre que a combinação que aparece na figura pode ser substituida por uma indutância equivalente dada por:

(b) De que forma as bobinas da figura 30-72 podem ser ligadas para que a indutância equivalente seja

Vamos supor que a taxa de variação da corrente é e calcular a fem total induzida no circuito formado pelas duas bobinas. Os campos magnéticos produzidos pelas duas bobinas apontam para a direita.

Quando a corrente aumenta, os dois mapos aumentam e as duas variações do fluxo induzem forças eletromotrizes de mesma polaridade.

Assim, a fem induzida no circuito é:

Simplificando...

que é a fem que seria produzida se as duas bobinas fossem substituídas por uma única bobina de indutância .

Legal, né? 😁

Para obter este novo valor da indutância equivalente, basta inverter as ligações da bobina 2 com a bobina 1. Isso faz com que os fluxos das bobinas tenham sentidos opostos: o aumento da corrente na bobina 1 aumenta o fluxo na bobina 1, mas esse aumento também aumena a corrente na bobina 2, o que produz um fluxo na bobina 1 oposto ao fluxo criado pela prórpia bobina.

O mesmo acontece com o fluxo na bobina 2. Assim, a fem induzida no circuito é:

Simplificando...

que é a fem que seria produzida se as duas bobinas fossem substituídas por uma única bobina de indutância .

E aí! o que achou? Responde Aí! 😉