Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.4 - Ex. 27
Dois fios longos e paralelos de cobre com de diâmetro, comduzem correntes de em sentidos opostos. (a) Se os eixos centrais dos fios estão separados por uma distância de , determine o fluxo magnético por metro de fio que existe no espaço entre os fios. (b) Quem porcentagem desse fluxo está no interior dos fios? (c) Repita o item (a) supondo que as correntes têm o mesmo sentido.
Passo 1
Fala aí! tudo certinho? 😁
O problema diz que dois fios muito longos (vamos aproximar por fios infinitos) conduzem uma corrente em sentidos contrários. Vamos posicionar o fio com corrente para baixo no eixo e o outro fio (corrente para cima) com seu eixo na reta . O raio dos fios é denotado por .
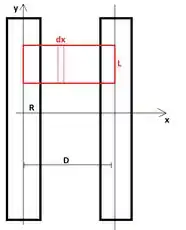
Queremos o fluxo por unidade de comprimento na região entre os fios .
Para isso, vamos considerar a região retangular (em vermelho) com base e altura . O fluxo nessa região:
representa a soma do campo devido aos dois fios. Como o fio da esquerda tem corrente para baixo e o da direita para cima, os campos gerados entre os fios terão mesmo sentido (para fora da figura, isto é, na direção positiva). Desta forma, os campos se somam:
Por fim, uma última simplificação que podemos fazer: note que há uma simetria com relação à reta . O fluxo de até é igual ao fluxo de até . Isso ocorre porque não importa qual fio escolhemos para colocar na origem do sistema de coordenadas: a simetria está lá! Assim,
Veja só! 👀
Passo 2
Note que entre e , o campo magnético criado pelo fio 1 (fio da esquerda com corrente para baixo) é diferente para (dentro do fio) e para (fora do fio). Dentro do fio, o campo magnético cresce linearmente com :
Já fora do fio, temos à expressão clássica:
Essas expressões foram todas deduzidas e trabalhadas no capítulo 29. Já para o fio 2 (da direita com corrente para cima):
Assim, o fluxo será
Fazendo as integrações:
Desta forma, o fluxo por unidade de comprimento entre os fios será:
Usando , , e , obtemos
Tranquilo até aqui? 😉
Passo 3
No item (b) queremos a porcentagem do fluxo calculado no item anterior que está no interior dos fios. Para isso, temos que considerar somente a integral de até :
Assim,
Substituindo os números:
Desta forma, a porcentagem será
Portanto, do fluxo está na região interna aos fios e na região externa.
Legal, né? 😊
Passo 4
No item (c) pergunta-se o que ocorreria se as correntes estivessem no mesmo sentido: neste caso, os campos estariam em sentidos contrários, de modo que a simetria em torno de faria com que o fluxo total fosse nulo:
E aí! o que achou? Responde Aí! 😁
Resposta
O fluxo seria nulo