Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.4 - Ex. 24
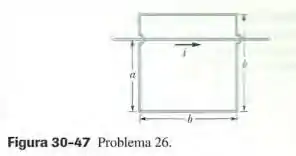
No sistema da Fig. 30-47, e . A corrente no fio retilíneo longo é dada por , onde está em ampères e em segundos. (a) Determine a força eletromotriz na espira quadrado no instante . (b) Qual o sentido da corrente induzida na espira?
Passo 1
O problema dá um fio que passa por uma espira quadrada de lado de modo que a corrente faz com que exista um campo magnético perpendicular ao plano da espira. Assim, haverá um fluxo magnético sobre ela. Como a corrente varia no tempo, o fluxo também vai variar, dando origem a uma força eletromotriz induzida: é ela que queremos calcular!
O primeiro passo é calcular o fluxo sobre a espira. Para isso, vamos adotar com convenção a normal saindo do plano da figura. Acima do fio o campo estará saindo da figura (fluxo positivo), enquanto abaixo do fio o campo estará entrando (fluxo negativo).
O campo, a uma distância do fio será
Assim, considerando faixar horizontais bem finas com espessura , o fluxo sobre ela será:
Assim, o fluxo total será:
Para escrever essa expressão eu considerei que o fluxo negativo abaixo do fio entre e ia cancelar com o fluxo positivo acima do fio. Desta forma, só precisei considerar o fluxo negativo entre e .
Passo 2
Agora vamos integrar para calcular o fluxo:
Pela lei de Faraday, a fem induzida é
Mas como segue que
Em :
Assim, com , , temos que
Passo 3
No item (b) devemos dizer qual o sentido da corrente induzida na espira. Por convenção, adotamos a normal à região limitada pela espira para fora da figura, de modo que o sentido positivo da corrente seria o anti-horário.
Como obtivemos , a corrente é positiva: sentido anti-horário!
Resposta
Sentido anti-horário