Em uma região do espaço onde não há corrente de condução nem de deslocamento, é impossível existir um campo elétrico uniforme que caia repentinamente até zero. Para comprovar essa afirmação, use o método da contradição. Suponha que essa hipótese seja verdade, a seguir mostre que ela contradiz uma lei da natureza.

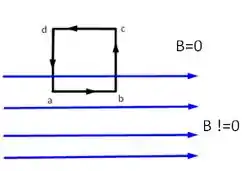
Na metade inferior de uma folha de papel, desenhe retas paralelas igualmente espaçadas para representar um campo magnético uniforme orientado da esquerda para a direita. Usa linhas tracejadas para representar um retângulo com o lado horizontal na região do campo magnético e o lado na metade superior da folha, em que .

Mostre que a integração ao longo do retângulo contradiz a lei de Ampère, equação (29.15) .

Como é inviável desenhar o problema seguindo exatamente as instruções do enunciado, mas vamos desenhar a região do campo elétrico da qual trata o problema que pode ser esquematizada da seguinte forma

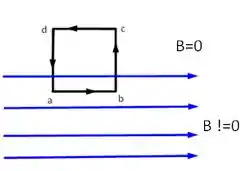
Temos que a lei de Ampère para esse caso é dada por

É igual a pois não temos corrente na região. Assim, usando a figura acima vamos considerar que para e para . Dessa forma, teremos

Mas nesse caso temos então , porém, nas nossas considerações tínhamos que . Nesse caso, podemos ver que isso contradiz e viola a lei de Ampère.