Dois fios paralelos infinitamente longos têm carga uniforme por unidade de comprimento e respectivamente. Os fios são paralelos ao eixo z. O fio carregado positivamente intercepta o eixo x em x = - a, e o fio carregado negativamente intercepta o eixo x em x =+a. (a) Escolha a origem como o ponto de referência onde o potencial é zero, e expresse o potencial em um ponto arbitrário (x, y) no plano xy em termos de x, y, l e a. Use esta expressão para encontrar o potencial em todos os pontos do eixo y. (b) Usando a = 5,00 cm e l = 5,00 nC/m, obtenha a equação para a superfície equipotencial no plano xy que passa através do ponto x = 1/4 a, y= 0. (c) Use um programa de planilha eletrônica para fazer um gráfico da superfície equipotencial encontrada na Parte (b).
Passo 1
Fala ai galera!! A figura abaixo representa o esquema:
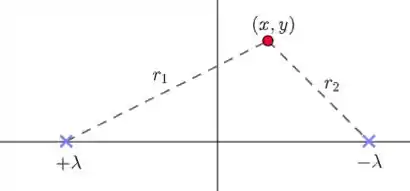
Lembre-se que o potencial elétrico a uma distância de um fio infinito é:
onde é a nossa referência para potencial nulo (no caso a origem).
Passo 2
- Temos que
- Usando os valores numéricos, temos
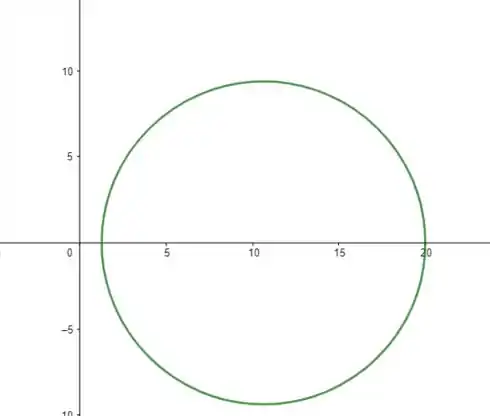
- A figura a seguir representa a equipotencial obtida:
Da geometria, temos que e . Logo,
No eixo , temos . Assim,
pois .
Passo 3
Assim, temos que que
Após fazer as simplificações, temos:
Bem trabalhosa essa questão, não? :D
Resposta
Ei, a resposta está no passo a passo :)