Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 23.1 - Ex. 66
Cargas puntiformes estão fixas nos vértices de um triângulo equilátero cujos lados tem comprimento de . Determine a energia potencial eletrostática deste sistema de cargas para os seguintes valores de carga: (a) , (b) e ; e (c) e . (Considere que a energia potencial seja zero quando as cargas estão muito afastadas.)
Passo 1
Fala galera, temos o seguinte esquema abaixo:
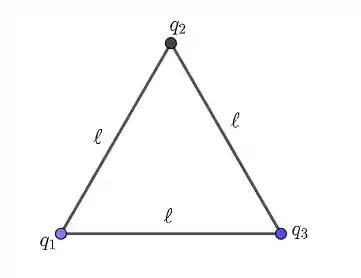
A energia potencial será dada por:
Passo 2
- Temos que
- Temos que
- Por fim,
Resposta
Exercícios de Livros Relacionados
Considere uma carga puntiforme q = 1,5 × 10 - 8C , e tome V = 0 no infinito. (a) Quais são a forma e as dimensões de uma superfície equipotencial que tem um potencial de 30V graças somente a q ? (b) E
A Fig. 26-25 mostra uma chapa não-condutora, infinita, com densidade superficial de carga positiva sobre um lado. (a) Qual é o trabalho realizado pelo campo elétrico da chapa, quando uma pequena carga
Quando um elétron se move de A até B ao longo da linha de campo elétrico mostrada na Fig. 26-24, o campo elétrico realiza um trabalho de 3,94 × 10 - 19J sobre ele. Quais são as diferenças de potencial
Uma carga q está uniformemente distribuída através de um volume esférico de raio R . (a) Fazendo V = 0 no infinito, mostre que o potencial a uma distância r do centro, onde rR , é dado por V = q e R 2
Uma casca esférica espessa de carga Q e densidade volumétrica de carga uniforme ρ está limitada pelos raios r , e r 2 , onde r 2r . Com V = 0 no infinito, determine o potencial elétrico V em função da