Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 88

Dois picos nevados estão H   =   850   m e h   =   750   m acima do vale que os separa . Uma pista de esquiação, com um comprimento total de   3,2   k m e uma inclinação média θ   =   30 ° , liga os dois picos (Fig. 8-59). (a) Um esquiador parte do repouso no cume do monte mais alto. Com que velocidade chega ao cume do monte mais baixo se não usar os bastões para dar impulso? Ignore o atrito . (b) Qual é o valor aproximado do coeficiente de atrito cinético entre a neve e os esquis para que o esquiador pare exatamente no cume do monte mais baixo?

Figura 8-59 Problema 72

Passo 1

a) Oi, galerinha! Tudo bom? Vamos resolver essa questão aplicando o princípio de conservação da energia mecânica:

K 1 + U 1 = K 2 + U 2

Como o esquiador parte do repouso, temos que a energia cinética incial é zero ( K 1 = 0 ), então

U 1 = K 2 + U 2

m g h 1 = 1 2 m v 2 + m g h 2

Isolando a velocidade, ficamos com

v 2 = 2 g h 1 - h 2

Como h 1 = H e h 2 = h

v 2 = 2 g ( H - h )

v = 2 g H - h

Para g = 9,8   m / s 2 , H = 850   m e h = 750   m ,temos que

v = 2.9,8 . 850 - 750

v = 44,27   m / s ≈ 44   m / s

Passo 2

b) A força de atrito é

f = μ k F N

onde μ k é o coeficiente de atrito cinético e F N é a força normal exercida pelo solo no esquiador.

Fazendo um esboço das forças envolvidas,

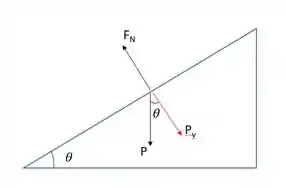
Temos que,

F N = P . c o s θ = m g c o s θ

Logo, f = μ k m g c o s θ e sua energia é dada por

∆ E T = f . d = μ k m g d c o s θ

Pela lei da conservação de energia para os 2 pontos. Nos 2 instantes a velocidade é nula, logo K 1 = K 2 = 0 e a ∆ U será igual a energia térmica produzida,

∆ E T = ∆ U

μ k m g d c o s θ = m g H - h

μ k = H - h d c o s θ

Para d = 3,2 . 10 3   m e θ = 30 °

μ k = 850 - 750 3,2.10 3 . cos ⁡ 30 °

μ k = 0,036

Resposta

a) A velocidade com que o esquiador chega ao cume do monte mais baixo é v ≈ 44   m / s .

b) O coeficiente de atrito cinético entre a neve e o esqui é μ k = 0,036 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um trenó de massa m é chutado em um lago congelado. O chute lhe dá uma velocidade inicial v. O coeficiente de atrito cinético entre o trenó e o gelo é μ k . Use considerações de energia para encontrar
Um corpo de 1,50 kg é mantido 1,20 m acima de uma mola vertical relaxada e sem massa, com uma força constante de 320 N/m. O corpo é jogado em cima da mola. (a) Quanto o corpo comprime a mola? (b) E se
Um bloco de massa m = 2,00 kg é preso a uma mola com constante elástica k=500N / m , como mostrado na Figura P7.15. O bloco é puxado para uma posição x i=5,00 cm para a direita do equilíbrio e solto d
Um bloco de 5,00 kg é colocado em movimento para cima em um plano inclinado com velocidade inicial de vi = 8,00 m/s (Fig. P7.21). O bloco chega ao repouso depois de percorrer d = 3,00 m ao longo do pl
Jonathan pedala uma bicicleta e chega a um morro de altura h . Na base do morro, ele está a uma velocidade v i . Quando chega ao topo do morro, ele está viajando a uma velocidade v f . Juntos, Jonatha