Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 16.1 - Ex. 1
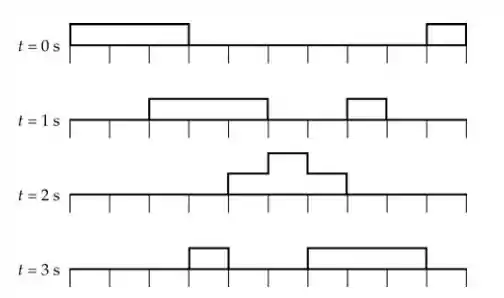
Dois pulsos de ondas retangulares viajam em sentidos opostos ao longo de uma corda. Em , os dois pulsos estão como mostrado na figura. Esboce as funções de onda para ; e .
Passo 1
Bora lá destruir mais esse capítulo! Você vai vencer essa, guerreirinho!
Pra essa questão, a gente tem que fazer o seguinte: determinar a posição de cada onda em cada momento. Se as ondas ficarem sobrepostas, os tamanhos vão somar! Beleza então, bora lá! Eu vou considerar o ponto mais à direita da primeira onda e o ponto mais à esquerda da segunda onda pra marcar a coordenada, e o ponto mais à esquerda da figura como origem. Aí embaixo tá tudo em centímetro, ok?
Em : e
Em : e . Ainda não tem superposição.
Em : e . Mas a gente tem que pensar no tamanho todo, então aqui vai ter superposição, porque o segundo vai ficar no meio do primeiro!
Em : e . Agora não tem mais superposição!
Passo 2
Aí a gente desenha! Considerando as superposições no momento em que , vamos ter que somar as amplitudes naquele intervalinho de até . O gráfico vai ficar assim, então!
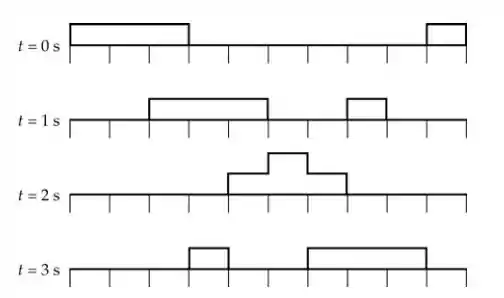
Resposta
