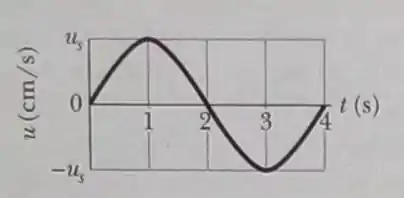
Uma certa onda transversal senoidal com um comprimento de onda de está se propagando no sentido positivo ele um eixo . A Figura mostra a velocidade transversal da partícula situada em em função do tempo; a escala do eixo vertical é definida por Qual é (a) a velocidade, (b)a amplitude e (c) a freqüência da onda? (d)Plote a onda entre e para o instante .

(b) Aqui, vamos lembrar de alguns resultados importantes com relação à equação geral da velocidade de uma onda progressiva. Como diz o enunciado, a velocidade é descrita por uma senoidal do tipo:

Como o gráfico que a representa nos mostra que, para , , a gente já pode concluir que:

Agora, você lembra como obtemos a equação da velocidade a partir da equação da posição ? Fizemos isso depois que derivamos a equação de com relação ao tempo . Então, pra gente obter a equação de a partir da de , basta a gente integrar com relação ao tempo. Fazendo isso, a gente obtém:

, sendo uma constante (como, em , , segue que ).

Então, temos que

A amplitude da onda, então, é igual à constante que multiplica o cosseno:

(c) Fomos rápidos dessa vez e já calculamos esse valor no passo 1. Essa freqüência vale .

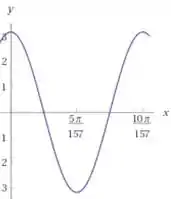
(d)Pra gente plotar a equação da onda entre e , no tempo , vamos, primeiro, substituir esse tempo na equação encontrada para :

Daí, podemos encontrar o seguinte gráfico para essa equação, cujo eixo das ordenadas está em centímetros: