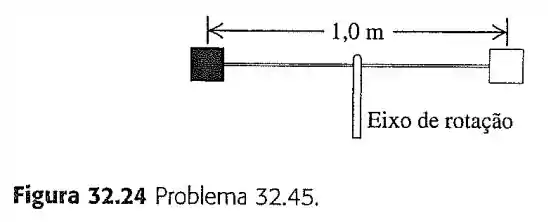
45- Dois refletores quadrados, cada qual com de lado e de massa, estão localizados em extremidades opostas de uma haste delgada, extremamente leve, de e que pode girar sem atrito e no vácuo em torno de um eixo perpendicular a ele no seu centro (Figura ). Esses refletores são suficientemente pequenos para serem tratados como massas puntiformes em cálculos de momento de inércia.

Ambos os refletores são iluminados em uma face por uma onda de luz senoidal com um campo elétrico de amplitude , que recai uniformemente sobre ambas as superfícies e sempre os atinge perpendicularmente ao plano das suas superfícies. Um refletor é coberto com um revestimento perfeitamente refletor. Qual é a aceleração angular desse dispositivo?

Como ambas as forças são atingidas no mesmo plano então a força resultante que gerará momento de rotação a haste será a força na superfície refletora diminuída pela força na superfície absorvedora, nos dando um o torque resultante de:

E a aceleração angular se correlaciona com o momento de giro da seguinte forma:

Onde é a inércia de giro total e que será igual a inércia de giro dos dois corpos, ou seja:

Então a aceleração angular será de:

E chegamos no final, que louco não. Vamos para mais uma questão