Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 85
O bloco da Figura possui massa de e o bloco possui massa de . O coeficiente de atrito cinético entre o bloco e a superfície horizontal é .
a) Determine a massa do bloco , sabendo que o bloco está se movendo para a direita e aumenta de velocidade com uma aceleração igual a .
b) Qual é a tensão em cada corda quando o bloco B possui essa aceleração?
Passo 1
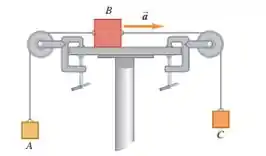
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte sistema:
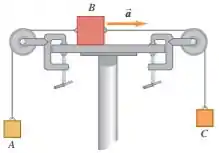
Onde o bloco da possui massa de e o bloco possui massa de . O coeficiente de atrito cinético entre o bloco e a superfície horizontal é .
Queremos determinar a massa do bloco , sabendo que o bloco está se movendo para a direita e aumenta de velocidade com uma aceleração igual a .
Também queremos determinar a tensão em cada corda quando o bloco B possui essa aceleração.
Para isso, temos que analisar todas as forças do sistema e aplicar a Segunda Lei de Newton:
Onde é a força resultante, é a massa e é a aceleração.
Passo 2
Mas antes de analisar cada situação, vamos olhar o sistema como um todo!
Nós temos as seguintes forças:
- a força tensora entre todos os fios: ela é a mesma em todos os pontos do mesmo fio, desprezamos sua massa;
- temos os pesos de e ( e , respectivamente) que são os que estão na direção do movimento, sendo que é maior, pois todo sistema se movimenta para a direita com descendo;
- e temos a força de atrito que age em , retardando o movimento e é proporcional ao seu peso.
Equacionando as forças, utilizando a segunda lei de Newton, teremos:
Onde , e são as massas dos blocos e , respectivamente.
Passo 3
- Aqui temos que descobrir a massa de , mas antes vamos achar a força de atrito entre a mesa e o bloco é:
- Agora vamos às tensões!
Onde é a força normal e é o coeficiente de atrito.
A aceleração que o conjunto se movimenta é .
E o peso de é
Agora é só substituir tudo e determinar a massa de :
Passo 3
Primeiro vamos calcular a tensão do fio que une os blocos e .
Olhando para o bloco temos duas forças: a tensão e o peso (que já calculamos). Então aplicando a segunda lei para esse bloco teremos:
Agora vamos olhar para o bloco .
Para a direita temos a tensão e para a esquerda temos a tensão e a força de atrito (ambas calculadas o outro item!).
A aceleração é para direita e vale .
Usando a segunda lei podemos determinar , saca só: