Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.3 - Ex. 48
Uma bola de beisebol é atirada verticalmente para cima. A força de arraste é proporcional a . Em termos de g, qual é o componente da aceleração quando a velocidade é igual à metade da velocidade terminal, supondo que a) ela se mova para cima? b) ela se mova de volta para baixo?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar o componente da aceleração quando a velocidade é igual à metade da velocidade terminal, supondo que a bola se mova pra cima ou pra baixo.
Nós sabemos que a bola foi atirada verticalmente pra cima, que a força de arraste é proporcional a e que a resistência do fluido é oposta a velocidade da bola.
Na metade da velocidade terminal, a força de atrito é do peso. Além disso, a força de atrito é menor que em cada caso e em cada caso a força é para baixo e a aceleração também é para baixo.
Vamos esboçar um diagrama de corpo livre da bola:
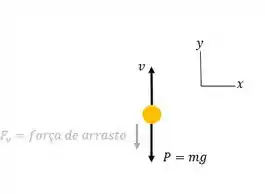
Considerando tudo isso, vamos usar a segunda lei de Newton para analisar as forças verticais agindo no movimento, considerando a força de arrasto , para encontrar a aceleração em cada caso.
Vamos lá!
Passo 2
Como podemos observar o diagrama de corpo livre, só temos componentes de força em . Assim, vamos aplicar a 2º lei de Newton sobre a bola no :
Onde é a força peso, é a força vertical resultante e . Então, temos:
Passo 3
Para calcular a velocidade terminal, consideramos a bola caindo. Agora, suponha que atingimos o ponto onde não há aceleração (ou seja, o ponto que ela para para começar a voltar):
Assim, vamos ter:
Onde é a velocidade terminal.
Passo 4
a) Quando atingir, em módulo, a metade da velocidade terminal, teremos:
Se a bola está subindo, a força de atrito está baixa, o sinal negativo signifiva uma desaceleração, então a força resultante é de e a aceleração é para baixo.
Passo 5
b) Quando atingir, em módulo, metade da velocidade terminal, para baixo, temos que a força de arrasto, , está para cima e a velocidade, , para baixo:
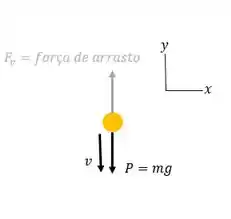
Então vamos, novamente aplicar a 2º lei de Newton na bola:
Substituindo e :
Como encontramos no passo , temos:
Então,
Enquanto se move para baixo, a força de atrito é para cima, e a magnitude da força é e a aceleração é para baixo.
Valeu, galera! Até a próxima! 😉