Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 4.Problemas - Ex. 43
Duas caixas, uma de massa e outra de , estão em repouso sobre a superfície sem atrito de um lago congelado, ligadas por uma corda leve . Uma mulher usando um tênis de solado áspero (de modo que ela possa exercer tração sobre o fio) puxa horizontalmente a caixa de com uma força que produz uma aceleração de .
- Qual é a aceleração da caixa de ?
- Desenhe um diagrama do corpo livre para a caixa de . Use esse diagrama e a segunda lei de Newton para achar a tensão na corda que conecta as duas caixas.
-
6 k g . Qual é a direção da força resultante sobre a caixa de ? Qual tem maior módulo, a força ou a ? - Use aparte e a segunda lei de Newton para calcular o módulo da força .
Passo 1
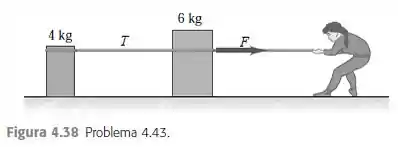
Eaee, belezinha?? Bom... o enunciado nos diz que duas caixas, uma de massa e outra de , estão em repouso sobre a superfície sem atrito de um lago congelado, ligadas por uma corda leve.
Uma mulher, usando um tênis de solado áspero (de modo que ela possa exercer tração sobre o fio), puxa horizontalmente a caixa de com uma força que produz uma aceleração de conforme a figura:
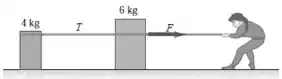
Queremos calcular a aceleração da caixa de , fazer o diagrama de corpo livre das duas caixas e calcular a força .
Para isso, teremos que utilizar a segunda Lei de Newton, onde a força resultante é dada por:
Onde é a massa e é a aceleração.
Passo 2
Vamos primeiro encontrar a aceleração da caixa de ...
Para isso, devemos saber que as duas caixas estão ligadas pela mesma corda,
Assim, o sistema se movimenta com a mesma aceleração. Então a caixa de possui uma aceleração de .
Agora vamos fazer o diagrama de corpo livre para cada uma das caixas!! 😉
Passo 3
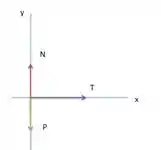
Três forças estão agindo sobre a caixa de :
- A força peso : vertical para baixo e de módulo , onde é a aceleração da gravidade;
- A força normal: vertical para cima . Seu módulo nesse caso é igual ao peso, pois o sistema está em repouso em relação ao eixo vertical;
- E por fim, a força de tração , horizontal para a direita, exercida pela caixa de sobre a caixa de .
- A força peso: vertical para baixo e de módulo ;
- A força normal: vertical para cima . Seu módulo nesse caso é igual ao peso, pois o sistema está em repouso em relação ao eixo vertical;
- A força exercida pela mulher, horizontal para a direita;
- E por fim, a força de tração , horizontal para a esquerda, exercida pela caixa de sobre a caixa de .
Com essas forças, podemos fazer o diagrama:
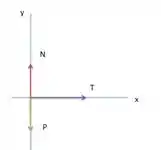
O módulo da força peso está representado pelo vetor verde, o módulo da força normal pelo vermelho, e da tração em roxo.
Passo 4
Na direção vertical temos que as duas forças e possuem módulos iguais:
Já na direção horizontal temos uma força resultante, a tração.
Como a caixa de movimenta com aceleração de , podemos usar a segunda lei de Newton e determinar a tração na caixa de :
Passo 5
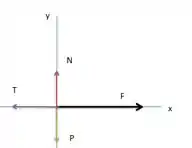
Agora vamos desenhar o diagrama para a outra caixa. Nela estão agindo quatro forças:
Juntando todas essas informações podemos construir o diagrama para a caixa de :
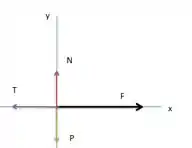
O módulo da força peso está representado pelo vetor verde, o módulo da força normal pelo vermelho, da tração em roxo e da força em preto.
Como o sistema acelera para a direita, então a força resultante também será para a direita. Sendo assim, o módulo maior é da força .
Passo 4
Usando a segunda Lei de Newton, temos:
- Na direção vertical temos que as duas forças e possuem módulos iguais:
- Na direção horizontal:
Assim o módulo da força é .
Resposta
