Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 66
Duas caixas de massas e , ligadas por um fio sem massa, estão sendo puxadas ao longo de uma superfície horizontal sem atrito, pela força de tensão de um segundo fio, como mostra a Figura 4-50. (a) Desenhe o diagrama de corpo libre das duas caixas separadamente e mostre que (b) Este resultado é plausível? Explique. Esta resposta faz sentido nos limites e Explique.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O diagrama de corpo livre, para a situação descrita, está exposto abaixo:
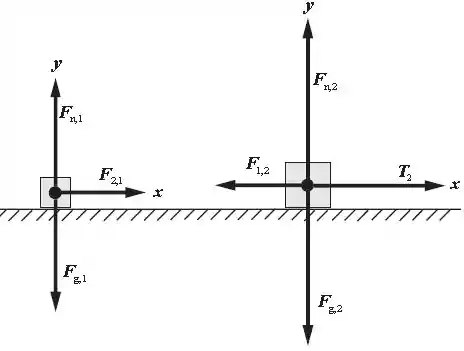
Aplicando a segunda lei de Newton na caixa da esquerda, temos:
Como , temos que:
Aplicando a segunda lei de Newton na caixa da direita, temos:
Como , temos que:
Como as caixas têm a mesma aceleração, temos que:
Fazendo a razão , temos:
Como dito no enunciado:
Passo 2
O resultado obtido no passo 1 é plausível pois a corda sujeita a , só sofre os efeitos de , porém a corda sujeita a , sofre os efeitos de e
Para avaliar os limites pedidos no item (b), podemos fazer algumas manipulações algébricas.
Temos que:
Se
Quanto maior a massa da segunda caixa, menor será a importância de e para o sistema.
Se
Resposta
Ei, a resposta está no passo a passo :)