Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 72
Uma corrente é constituída de , cada um de massa . A corrente está sendo puxada para cima por uma força aplicada por sua mão no elo superior, dando à corrente uma aceleração para cima de Encontre (a) a magnitude de força F exercida no elo superior pela sua mão; (b) a força resultante em cada elo; e (c) a magnitude da força que cada elo exerce no elo imediatamente abaixo.
Passo 1
a) Oi pessoal, tudo bem? Vamos analisar essa questão. Temos uma corrente sendo puxada para cima por uma força de , sendo que essa corrente adquire a aceleração .
A primeira pergunta que ele faz é qual é a magnitude de . Aqui a gente precisa pensar que , apesar de estar sendo aplicada em um só elo, faz a aceleração de todos os elos serem a mesma. Então a gente pode pensar que a corrente é um objeto só: um conjunto formado pelos elos.
E sobre esse objeto único, há uma força para cima e há também a força peso para baixo, que existe porque a corrente tem a massa total , que é a soma das massas da corrente de cada elo. Sendo .
O diagrama de corpo livre, para a situação descrita, está exposto abaixo:
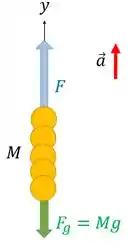
Aplicando a segunda lei de Newton no conjunto que forma a corrente, na direção :
Lembrando que :
E que :
Isolando e substituindo nossos dados:
Passo 2
b) Agora ele quer a força resultante em cada elo. O que a segunda lei e Newton diz? Ela diz isso aqui:
Ela diz que para um objeto, a força resultante é igual ao produto entre a massa do objeto e a aceleração que ele tem .
A massa de cada elo é . E a aceleração sobre cada elo é a mesma aceleração sobre a corrente . E precisa ser a mesma para todos os elos, caso contrário eles não estariam se movendo juntos, e a corrente poderia, por exemplo, ser arrebentada.
Logo, se a gente aplicar a segunda lei de Newton para um elo, a gente vai encontrar a força resultante sobre cada um deles porque todos têm a mesma massa e a mesma aceleração.
Vamos aplicar a segunda lei de newton para a direção , onde estão todas as forças e a aceleração, e achar a magnitude de , que vale para cada elo:
Substituindo os dados:
Passo 3
c) Agora a gente quer saber a força de contato que um elo exerce no elo que está abaixo dele. Para isso, vamos fazer o diagrama de corpo livre desses elos:
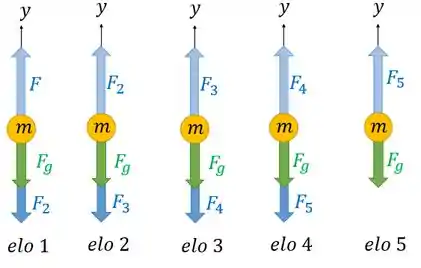
Todos os elos tem a mesma massa e mesma força peso sobre eles.
No elo 1 temos a força que puxa o conjunto para cima. Só que esse elo 1 puxa o de baixo com uma força . Só que pela terceira lei de Newton, se esse elo1 puxa o elo 2 para cima, o elo 2 vai puxar o elo 1 para baixo com a mesma magnitude .
E isso acontece com os outros elos, o elo 2 puxa o elo 3 para cima com uma força , aí pela terceira lei de Newton, o elo 3 também vai puxar o elo 2 para baixo. O mesmo acontece para o elo 3, 4 e 5. A diferença é que o elo 5 não puxa ninguém para cima. Logo, nele só há a força que é exercida pelo elo 4.
Vamos então aplicar a segunda lei de Newton para cada elo, lembrando que :
Passo 4
Lembra que sabemos quem é lá do passo 1, então temos . Podemos substituir isso em :
Isolando e substituído os dados:
Para , podemos usar e a expressão que acabamos de achar :
Passo 5
Para , usamos e a expressão que encontramos :
Para , podemos isolar de :