Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 87
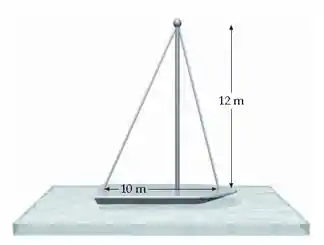
O mastro de um veleiro é preso à proa e à popa por tirantes metálicos de aço inoxidável, um frontal e o outro traseiro, com as bases separadas de (Figura 4-61). O mastro de de comprimento pesa e se mantém na vertical em relação ao convés. O mastro está posicionado atrás da base do tirante frontal. A tensão neste tirante é de 500 N. Encontre a tensão no outro tirante e a força que o mastro exerce sobre o convés.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O diagrama de corpo livre do problema está exposto na figura abaixo:
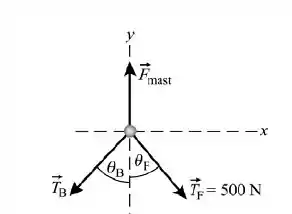
Aplicando , temos:
Pelos aspectos geométricos podemos achar e :
Portanto, temos que:
Passo 2
Aplicando a segunda lei de Newton na vertical, temos:
Logo, a força no mastro é dada por:
A força que o mastro exerce sobre o convés, é dada pela soma do seu peso com a força no mastro.