Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 81
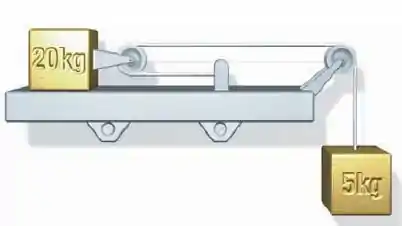
Um bloco de , com uma polia presa a ele, desliza ao longo de um trilho sem atrito. Ele está conectado, por um fio sem massa, a um bloco de , como mostra o arranjo da Figura 4-59. Encontre (a) a aceleração de cada bloco e (b) a tensão no fio.
Passo 1
a) Oi pessoal, tudo bem? A ideia aqui é perceber que como não há atrito, o bloco de vai cair, e vai puxar o outro bloco de .
Aqui nesse item ele quer a aceleração de cada bloco.
Mas percebe uma coisa. Temos uma polia ali presa no bloco de . A corda envolve ela e se liga a plataforma. Se nessa corda temos uma tensão de , o diagrama dessa polia seria:
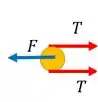
Porque temos a corda saindo dela para se ligar ao bloco mais leve e para se ligar a plataforma, como a tensão em uma corda é a mesma em todos os pontos, há duas tensões para esquerda puxando a polia.
E a polia aplica uma força sobre o bloco, o puxando para a direita, logo, pela terceira lei de Newton, há uma força sobre a polia aplicada pelo bloco a puxando para a esquerda. Então com que força a polia vai puxar o bloco mais pesado?
Essa polia está parada, então a força com que ela vai puxar o bloco mais pesado deve ser igual a força total que está para a direita, ou seja, temos que ter . Ou seja, essa polia puxa o bloco de com uma força de .
Agora a gente tem todas as informações para fazer o diagrama de corpo livre para os dois blocos:
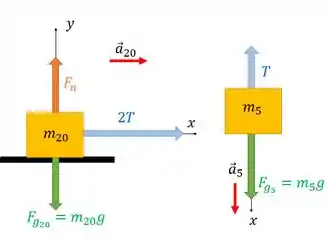
A gente colocou no sentido da aceleração em cada caso só para facilitar as contas. Percebe que a aceleração é resultado de uma força resultante no seu sentido, por isso as forças no sentido da aceleração aparecem maiores do que as que estão nos sentido inverso.
Temos tensão onde a gente tem a cordinha. E a força que vale puxando o bloco. Cada caixa tem sua força peso por ter massa. E a caixa da esquerda tem uma força normal por estar em contato com a superfície.
Bora equacionar essas forças através da segunda lei de Newton para achar .
Passo 2
Aplicando a segunda lei de Newton no bloco de temos:
Aplicando a segunda lei de Newton no bloco de temos:
Mas a gente não pode dizer que , porque o bloco de não está ligado à corda como o bloco de , mas à polia.
Então o que a gente vai fazer?
Passo 3
Podemos tentar relacionar essas acelerações usando o deslocamento dos blocos.
A gente pode usar a equação da posição para aceleração constante, para achar os desclocamentos desses dois blocos em um tempo :
Se a gente considerar que os dois saíram do repouso, para os dois, e o deslocamento de cada um fica:
Dividindo as duas equações, temos:
Agora uma dica: quando a gente tem um elemento (no caso, o bloco de ) ligado a polia e a polia é envolvida pela corda. Se a corda está ligada a outro elemento móvel (o bloco de ) e a um elemento fixo (no nosso caso, a plataforma), o deslocamento do elemento móvel ligado a corda é duas vezes maior do que o deslocamento do elemento móvel ligado a polia.
Imagina que o deslocamento do bloco de quando chega a polia, vai se “dividir” entre os dois pedaços da corda para puxar essa polia. Aí o bloco vai ser mover apenas .
Susbtituindo isso na nossa razão:
Passo 4
Aí vamos substituir isso na equação do passo 2
Agora vamos isolar da equação :
E substituir em :
Isolando
Substituindo os valores, temos:
E para o outro bloco:
Passo 5
O item (b), nos pede a tensão Com os cálculos do Passo 5, achamos através da equação que: