Duas cargas positivas iguais, , estão no eixo , uma carga puntiforme está em e a outra está em . (a) Mostre que, no eixo , a componente do campo elétrico é dada por . (b) Mostre que, próximo à origem, onde é muito menor que , . (c) Mostre que, para valores de muito maiores que , . Explique por que poderíamos esperar este resultado mesmo sem calculá-lo tomando o limite apropriado.
Passo 1
- Veja o esquema a seguir:
- Para , podemos desprezar o em . Assim,
- Para , podemos desprezar o em . Assim ,
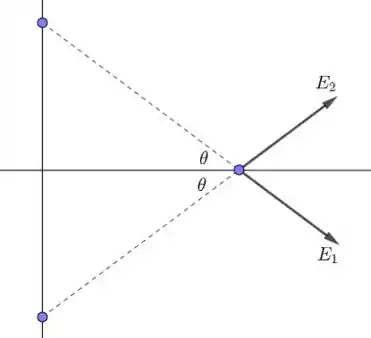
Veja que:
Note que o campo elétrico no eixo vai ser anulado. O campo resultante no eixo será:
Da figura,
Assim,
Passo 2
Passo 3
Deveríamos esperar esse resultado, mesmo sem calcular, pois a grandes distâncias, praticamente se perde qualquer noção de que as cargas estão separadas. Assim, tudo se passa como se tivéssemos uma partícula de carga .
Resposta
Ei, a resposta está no passo a passo :)