Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.Problemas Adicionais - Ex. 59
Três partículas carregadas formam um triângulo: a partícula 1, com uma carga = 80,0 nC, está no ponto (0; 3,00 mm) ; a partícula 2, com uma carga , está no ponto (O; -3,00 mm) e a partícula 3, com uma carga = 18,0 nC, está no ponto (4,00 mm; 0). Em termos dos vetores unitários, qual é a força eletrostática exercida sobre a partícula 3 pelas outras duas partículas.
(a) para = 80,0nC;
(b) para = -80,0 nC.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
O enunciado quer saber qual a força exercida na carga 3 devido às outras duas cargas. Quando nós ouvimos falar em força devido à carga elétrica devemos lembrar da Lei de Coulomb!
Relembrando a Lei de Coulomb:
Em que e são duas cargas, é a constante de Coulomb e é a distância entre as duas cargas.
Tranquilo, não é? 😊
Passo 2
Item (a)
A força que a partícula 3 está submetida é a soma das forças relativas às partículas 2 e 1 (não se esqueça que é a soma vetorial, ok?). Então podemos dizer que a força total presente na figura 3 é .
Agora olhe para a figura abaixo:
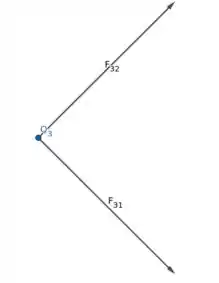
Vemos nessa figura as forças exercidas pelas partículas 1 e 2, como todas as partículas são positivas e as partículas 1 e 2 têm mesmo módulo, as forças são repulsivas e tem as direções indicadas na figura acima. Agora olhe a figura abaixo:
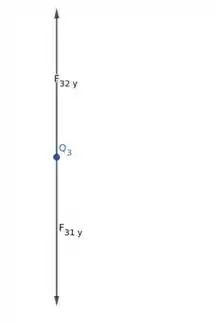
Nessa figura apenas indiquei as componentes do eixo y das duas forças. Viu o que eu vi? as componentes y são iguais! Isso irá nos poupar bastante tempo. Agora sabemos que a força terá o mesmo sentido do eixo x. Portanto devemos apenas calcular os módulos das forças, pois a direção já sabemos.
Legal, né? 😉
Passo 3
Para saber o módulo da força devemos saber a distância entre a partícula 3 e as partículas 1 e 2. Pela simetria, vemos que a distância é a mesma entre a partícula 3 e a partícula 1 e entre a partícula 3 e a partícula 2. Como vamos calcular essa distância? Pelo teorema de Pitágoras.
Agora como sabemos as distâncias, as cargas e a constante de Coulomb que é , podemos substituir na Lei de Coulomb e saber a força relativa a carga 3! Lembrando que devemos multiplicar os módulos das forças pelo cosseno do ângulo entre a força e o eixo x, já que queremos somar apenas as componentes no eixo x.
Como vamos saber o cosseno do ângulo entre as forças e o eixo x? Olhando paras as partículas vemos o famoso triângulo de lados 3, 4 e 5:
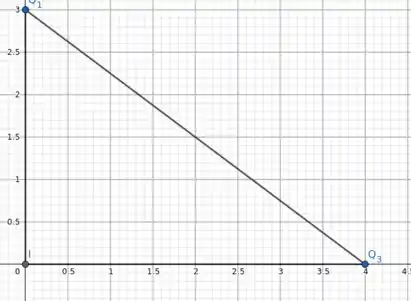
O ângulo entre as forças e o eixo x é o mesmo ângulo do triângulo onde a carga 1 está. Como esse triângulo é retângulo, achar o cosseno de um ângulo é muito fácil. Chamaremos esse ângulo de .
Agora, substituindo na Lei de Coulomb:
Substituindo os valores que descobrimos, e sabemos que o vetor está na mesma direção do eixo x, vemos que
Tranquilo até aqui? 😎
Passo 4
item (b)
A diferença entre o item a e o item b é que no item b a carga da partícula 2 é negativa, então a força entre a partícula 3 e 2 é atrativa. Olhe o diagrama com as forças abaixo:
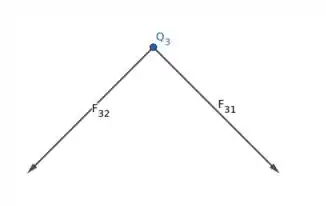
Como as partículas 1 e 2 têm mesmo módulo, e se desenharmos as componentes x das duas forças veremos que elas se anularam da mesma forma que as componentes y se anularam no item a. Portanto, a direção será a mesma do eixo y (só que com sinal negativo porque está para baixo). então, fazendo a mesma conta do item anterior, porém agora temos que multiplicar os módulos das forças pelo cosseno do ângulo entre as forças e o eixo y. Esse ângulo, que chamaremos de , é o complementar do ângulo , portanto, é igual ao outro ângulo do triângulo mostrado na figura do item a. Portanto,
Então, substituindo os valores que já sabemos (lembrando que substituiremos o módulo da carga 2 já que estamos calculando apenas o módulo, pois o sentido já sabemos).
Substituindo todos os valores encontraremos que .
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
(a)
(b)