Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 50

Duas cargas puntiformes positivas + q estão no eixo y em y = + a e y = - a . Uma esfera de massa m e carga - q possui um furo por onde passa um fio. Ela desliza sem atrito ao longo do fio estivado, paralelo ao eixo x . Seja x a posição da esfera. (a) Mostre que, para x ≪ a , uma força restauradora linear é exercida sobre a esfera (uma força que é proporcional a x e dirigida para a posição de equilíbrio em x = 0 ) e, portanto, a esfera executa movimento harmônico simples. (b) Determine o período do movimento.

Passo 1

  1. Observação: Há um erro no enunciado; a esfera deveria ter carga - q !! Caso fosse + q , o movimento não seria harmônico simples.

    2. Considerando a carga da esfera igual a - q , então temos o seguinte esquema:

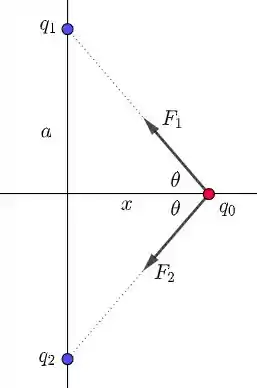
    Veja que, pela simetria, a força irá apontar no eixo x . Como

    F 1 = F 2 = k q 2 d 2

    onde

    d = x 2 + a 2

    E

    cos ⁡ θ = x d

    Sendo assim, segue que

    F r = 2 F 1 cos ⁡ θ = 2 k q 2 d 2 ⋅ x d F r = 2 k q 2 d 3 x

    Passo 2

    Como x ≪ a , segue que

    d = x 2 + a 2 ≈ a

    pois x 2 + a 2 ≈ a 2 . Logo,

    F r = 2 k q 2 a 3 x

    Passo 3

  2. Lembrando que se temos um MHS do tipo F = K x , então seu período será:

T = 2 π m / K

no nosso caso, nossa “constante elástica”, será 2 k q 2 / a 3 . Logo,

T = 2 π m 2 k q 2 / a 3 T = 2 π m a 3 2 k q 2

Resposta

  1. Demonstração
  2. T = 2 π m a 3 / 2 k q 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três cargas puntiformes estão dispostas ao longo do eixo X a carga Q 1=+3,0μ C está na origem e a carga Q 2=- 5,0μ C está em x=0,200m . A carga Q 3=+8,0μ C , onde que Q 3 estará localizado quando a fo
Em uma nuvem de tempestade, pode haver cargas elétricas de + 40,0C próximas ao topo da nuvem e – 40,0C na parte inferior. Essas cargas são separadas por 2,00k m . Qual é a força elétrica sobre a carga
Na Fig. 21-27a, a partícula 1 (de carga q 1 ) e a partícula 2 (de carga q 2 ) são mantidas fixas no eixo x , separadas por uma distância de 8,00c m . A força que as partículas 1 e 2 exercem sobre uma
Na Fig. 21-31, as partículas 1 e 2 , de carga q 1=q 2=+3,20 × 10 - 19C , estão no eixo y , a uma distância d=17,0c m da origem. A partícula 3 , de carga q 3=+ 6,40 ×10 - 19 C , é deslocada ao longo do
A Fig. 21-31 mostra um sistema de quatro partículas carregadas,com θ=30,0 ° e d=2,00c m . A carga da partícula 2 é q 2=+ 8,00 ×10 - 19C ; a carga das partículas 3 e 4 é q 3=q 4=-1,60 × 10 - 19C . (a)