Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas desafioadores - Ex. 106
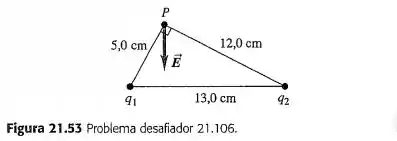
Duas cargas são colocadas como indica a Figura . O módulo de é igual a , porém não conhecemos seu sinal e nem o valor da carga . O campo elétrico resultante no ponto aponta para o sentido negativo do eixo . Considerando os possíveis sinais diferentes para as cargas e , existem quatro possíveis diagramas para representar os campos elétricos e produzidos por e . Faça desenhos mostrando esses quatro diagramas possíveis. Usando os desenhos da parte e a direção e o sentido de , determine os sinais das cargas e . Calcule o módulo do campo elétrico .
Passo 1
O sentido das forças exercidas pelas cargas e dependerá do sinal delas. Então, para cada combinação das cargas:
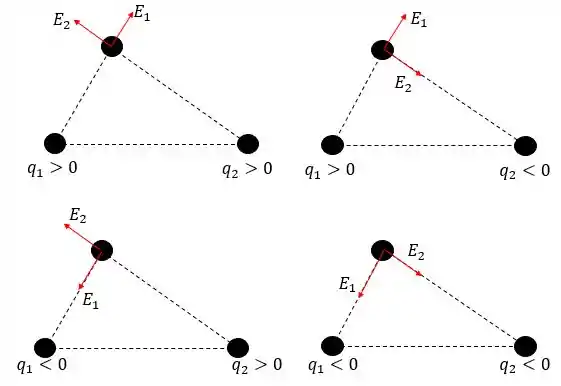
Tal que a combinação que corresponde ao campo elétrico no ponto é a última (diagrama do lado direito parte inferior).
Passo 2
Como foi determinado que o campo elétrico deriva do esquema:
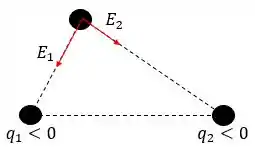
Então é possível ver que e .
Passo 3
Ao observar o sentido do campo resultante, um detalhe importante deve ser percebido: as componentes horizontais dos campos e se anulam para que seja vertical.
Portanto, podemos fazer um esboço das componentes:
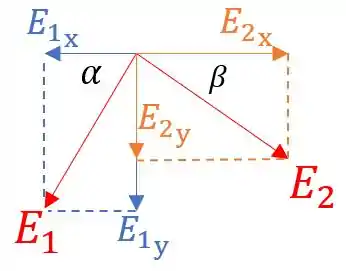
Conseguimos fazer a seguinte relação:
Tal que:
Onde:
E
Logo, substituindo na equação:
Tal que:
Então, isolando a variável de interesse:
Logo, usando a equação de equilíbrio:
Tal que:
Portanto:
Resposta
e