Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas desafioadores - Ex. 105d

Três cargas são colocadas como indica a Figura . O módulo de é igual a , porém não conhecemos seu sinal nem o valor da carga . A carga é igual a e a força resultante sobre aponta para o sentido negativo do eixo . Considerando os possíveis sinais diferentes para as cargas e , existem quatro diagramas de forças possíveis para representar as forças e exercidas por e sobre a carga . Faça os desenhos mostrando esses quatro diagramas possíveis. Usando os desenhos da parte e a direção e o sentido de , determine os sinais das cargas e . Calcule o módulo de . Calcule o módulo da força resultante que atua sobre .

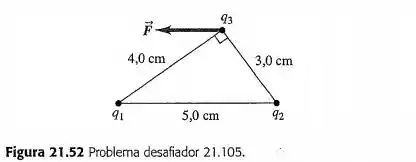
Passo 1

Para a última parte, devemos analisar as componentes horizontais das forças que resultam em :

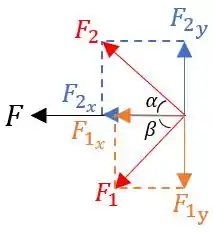
Logo:

Onde:

E

Passo 2

Logo, substituindo na equação:

Então, substituindo os valores:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Campo elétrico de axônios. Um sinal nervoso é transmitido através de um neurônio quando um excesso de íons de N a + subitamente entra no axônio, uma parte longa e cilíndrica do neurônio. Axônios possu

Se dois elétrons estão cada um a uma distância igual a 1,50 × 10 - 10m de um próton (Figura E21.45), encontre o módulo, a direção e o sentido da força elétrica resultante que eles irão exercer sobre o

Duas partículas cujas cargas são q 1 = 0,500n C e q 2 = 8,0n C estão separadas por uma distância de 1,2m . Em que ponto entre as cargas o campo elétrico resultante das duas cargas é igual a zero?

A carga puntiforme q 1 = - 5,00n C está na origem e a carga puntiforme q 2 = + 3,00n C está sobre o eixo x em x = 3,00c m . O ponto P está sobre o eixo y em y = 4,00c m . (a) Calcule os campos elétric

Uma carga puntiforme negativa q 1 = 4,00n C está sobre o eixo x no ponto x = 0,60m . Uma segunda carga puntiforme q 2 está sobre o eixo x no ponto x = - 1,20m . Determine o módulo e o sinal de q 2 par