Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 8.Problemas - Ex. 13

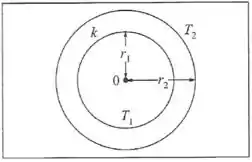
Duas esferas metálicas concêntricas, de raios r 1 e r 2 > r 1 , são mantidas respectivamente às temperaturas T 1 e T 2 , e estão separadas por uma camada de material homogêneo de condutividade térmica k . Calcule a taxa de transmissão de calor por unidade de tempo através dessa camada. Sugestão: Considere uma superfície esférica concêntrica intermediária de raio r ( r 1 < r < r 2 ) e escreva a lei de condução do calor através dessa superfície . Integre depois em relação a r , de r = r 1 até r = r 2 .

Passo 1

A ideia aqui é a seguinte: nós vamos calcular a taxa Φ de transferência de calor por uma casca esférica de raio r e espessura d r .

A diferença de temperatura entre as faces dessa casca esférica é d T , então:

Φ = k A d T d r

E a área de superfície é A = 4 π r 2 , então:

Φ = k 4 π r 2 d T d r

Essa taxa de transferência de calor deve ser a mesma em todos os pontos da esfera (seja para uma casca ou para uma camada).

Essa é uma equação diferencial separável que nós podemos resolver para encontrar Φ .

Passo 2

Começamos separando as variáveis:

Φ d r r 2 = 4 π k   d T

E agora vamos integrar quando r varia de r 1 até r 2 e T varia de T 1 até T 2 :

Φ ∫ r 1 r 2 d r r 2 = 4 π k ∫ T 1 T 2 d T

Agora é só resolver as integrais:

Φ   - 1 r r 2 r 1 = 4 π k T 2 - T 1

Φ 1 r 1 - 1 r 2 = 4 π k T 2 - T 1

E simplificando um pouco:

Φ r 2 - r 1 r 1 r 2 = 4 π k T 2 - T 1

Então:

Φ = 4 π k T 2 - T 1   r 1 r 2 r 2 - r 1

Resposta

A lei de condução de calor poro unidade de tempo é Φ = 4 π k T 2 - T 1   r 1 r 2 r 2 - r 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carpinteiro constrói uma porta de madeira maciça com dimensões de 2,0m × 0,95m × 5,0c m . Sua condutividade térmica é k = 0,120 W / m ⋅ K . A película de ar sobre a superfície interna e a película
Três barras, uma de cobre, uma de latão e outra de aço, são soldadas juntas em uma armação em forma de Y . A área da seção reta de cada barra é 2,0c m 2 . A extremidades livres das barras de latão e d
Uma barra está inicialmente a uma temperatura uniforme de 0° C . Uma de suas extremidade é mantida a 0° C e a outra é colocada em contato com vapor d’água a 100° C . A superfície da barra é isolada de
Calcule a razão entre a perda de calor de uma janela simples com área de 0,15m 2 e a perda de calor de uma janela dupla com a mesma área. A espessura do vidro de uma janela simples é 4,2m m , e o espa
Tempo necessário para um lago congelar.a) Quando a temperatura do ar é 0° C , a água da superfície de um lago congela e froma uma camada de gelo. Por que o gelo não se forma no volume total do lago?b)