O diagrama indicador da figura, onde a pressão é medida em e o volume em , está associado um ciclo descrito por um fluido homogêneo. Sejam , e respectivamente o trabalho, quantidade de calor e variação de energia interna do sistema associados com cada etapa do ciclo e com o ciclo completo, cujos valores (em ) devem ser preenchidos na table abaixo.
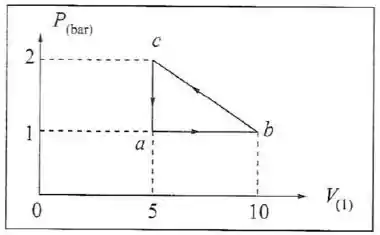
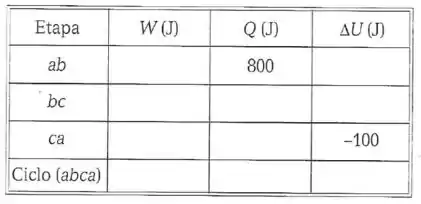
Passo 1
Nosso objetivo é preencher a tabela com valores em joules. Isso que dizer que a pressão deve estar em Pascal, e o volume deve estar em metros cúbicos.
Vamos converter os valores que aparecem no gráfico, sabendo que:
Então:
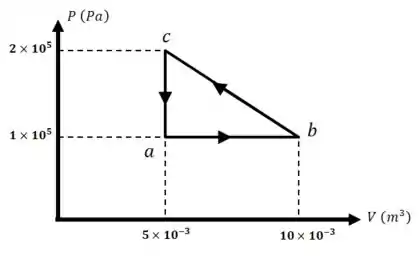
Passo 2
Beleza, agora vamos usar o gráfico para preencher a primeira coluna da tabela.
O trabalho no trecho é igual à área desse retângulo:
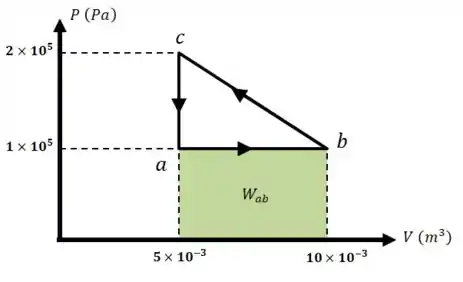
No trajeto , temos que somar essa área à área do triângulo :
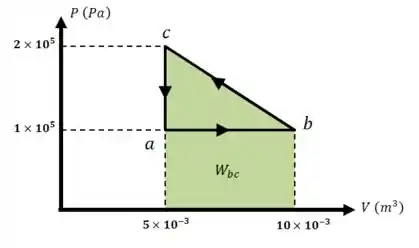
E o sinal negativo aparece porque o trajeto aponta no sentido de redução do volume. Isso quer dizer que o trabalho é realizado sobre o gás.
E no trajeto , como o volume permanece constante, o trabalho é nulo. Então a tabela fica assim:
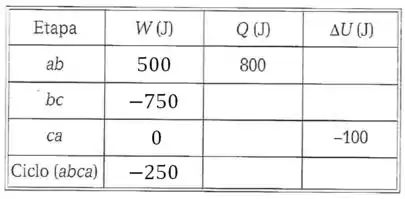
Na última linha, só precisamos somar os trabalhos em cada etapa.
Passo 3
Já podemos usar a primeira lei da termodinâmica para calcular a variação de energia interna na etapa :
Mais tarde, na etapa , a variação de energia interna é . Então, para o ciclo completo, temos:
Mas para o ciclo completo, a variação de energia interna deve ser nula, então:
E assim completamos a última coluna:
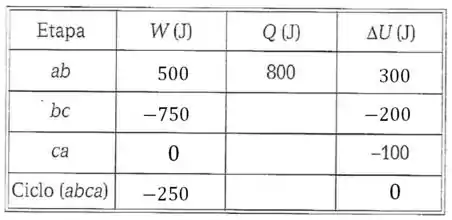
Passo 4
Para preencher a segunda coluna, vamos usar a primeira lei da termodinâmica.
Para a etapa :
Para a etapa :
E para o ciclo completo:
Então a tabela completa fica assim:
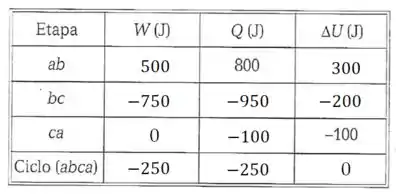
Resposta
Ver tabela.