Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 12.Exercícios - Ex. 5

Duas esferas uniformes, cada uma com massa igual a 0,260 kg, estão fixas nos pontos A e B (Figura El2.5). Determine o módulo, a direção e o sentido da aceleração inicial de uma esfera uniforme com massa 0,010 kg quando ela é liberada do repouso no ponto P e sofrendo apenas atrações gravitacionais das esferas situadas em A e B.

Passo 1

Faaaaala meu povo, bora iniciar mais um livrinho com a gente!

Para essa questão, temos que a massa da esfera que está no ponto P não irá interferir, pois temos que a aceleração da gravidade é dada por:

g = G M r 2

Assumindo que r seja a distância entra as esferas, e M sendo a massa da esfera de 0,260   k g , teremos então a aceleração no ponto P . Assumiremos o valor da constante gravitacional sendo:

G = 6,67 × 10 - 11 N m 2 / k g 2

Assim, substituindo os valores temos:

g = ( 6,67 × 10 - 11 ) ( 0,260 ) 10 × 10 - 2 2

g = 1,7342 × 10 - 9     m / s 2

Belezinha? Bora continuar.

Passo 2

Fazendo o diagrama de corpo livre, teremos as acelerações dessa forma:

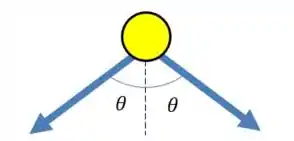
Repare que os ângulos são iguais porque os triângulos são equivalentes. Como as acelerações são iguais iremos ter apenas a componente vertical, ambas apontando para baixo. Usando a regra do seno e cosseno, temos:

g y = g × cos ⁡ θ

Mas quem é o cosseno de θ ? O cosseno de θ será igual ao cateto adjacente sobre hipotenusa, assim:

cos ⁡ θ = 6 10 = 3 5

Assim:

g y = 1,7342 × 10 - 9 × 3 5

g y = 1,04 × 10 - 9   m / s 2

Temos então que a aceleração total será:

g t o t a l = 2 g y

g t o t a l = 2,08 × 10 - 9   m / s 2

Tudo certinho? Te vejo na próximaaaaa!

Resposta

g t o t a l = 2,08 × 10 - 9   m / s 2

Exercícios de Livros Relacionados

Cem gramas de manteiga na Terra possuem a mesma quantidade de manteiga que cem gramas em Marte? O que você diria sobre um quilograma de manteiga? Explique
Na órbita elíptica do cometa Halley, indicada na Figura 12.21a, a gravidade do Sol faz o cometa cair aproximando-se do Sol do afélio para o periélio. Porém, qual é o efeito responsável pelo afastament
Se todos os planetas tivessem a mesma densidade média, como a aceleração da gravidade na superfície de um planeta dependeria de seu raio?
Uma empresa de comunicações deseja colocar um satélite em órbita de modo que ele sempre sobrevoe a Terra ao longo do paralelo 45 (latitude norte de 45°). Isso significa que o plano da órbita não passa
Muitas pessoas acreditam que astronautas em órbita não sentem seu peso porque estão “fora da atração da gravidade terrestre”. Qual deveria ser a distância entre uma espaçonave e a Terra para que ela r