Devemos começar lembrando que para resistores em série, as tensões são diferentes e a corrente é a mesma.

1. Esboçando o circuito, temos que:



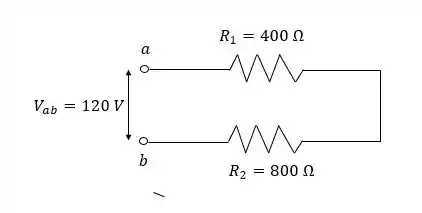
Assim, temos que a resistência equivalente desse circuito é igual a soma das resistências:

Agora podemos calcular a corrente que circula através da Primeira Lei de Ohm:

Para calculara a corrente:

Substituindo o valor da tensão e da resistência equivalente que encontramos :

Esta é a corrente que circula pelos dois resistores

Passo 2

2. A potência dissipada em um resistor é dada pela seguinte equação:

Como a corrente é a mesma nos dois resistores, a potência dissipada em cada lâmpada é dada por:

E

Passo 3

3. E a potencia total dissipada nas duas lâmpadas:

a potência total dissipada em ambas as lâmpadas.

Observe que o módulo da potência fornecida pela fonte é:

Ou seja, a energia fornecida pela fonte é igual a .

Passo 4

4. Para resistores colocados em paralelo, temos a mesma tensão, porém correntes diferentes. O circuito é esboçado na figura abaixo:



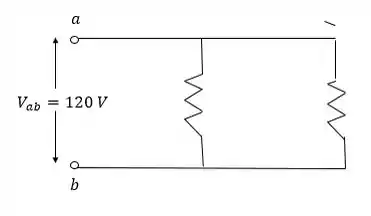
Agora podemos calcular a corrente que circula através da Primeira Lei de Ohm:

Para calculara a corrente:

Sendo que a tensão é a mesma em cada um dos resistores :

Observe que cada corrente é maior que a corrente quando os resistores são conectados em série.

Passo 5

A potência dissipada em um resistor é dada pela seguinte equação:

5. E, nesse caso, a potência dissipada em cada lâmpada:

E

Passo 6

6. Agora, vamo calcular a potencia total dissipada:

Observe que a corrente total consumida pela linha é . A fonte de tensão fornece uma potência igual a , que é igual à potência total dissipada pelas lâmpadas.

Passo 7

7. A lâmpada que está dissipando mais energia brilha mais intensamente.

Considerando todas as potências que calculamos, a lâmpada que dissipa mais potência é a de , no caso em que ela está ligada em paralelo.

Passo 8

8. Enquanto o sistema que dissipa mais potência é o colocado em paralelo, pois no total dissipa , enquanto o sistema em série dissipa apenas .