Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 8.Problemas - Ex. 78
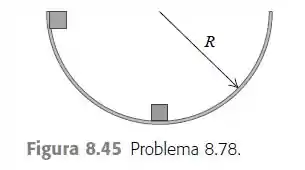
Duas massas idênticas são liberadas do repouso em um recipiente hemisférico liso e raio , a partir da posição indicada na Figura . Despreze o atrito entre as massas e a superfície do recipiente. Se elas colarem ao colidirem, que altura acima da parte inferior do recipiente as massas atingirão após a colisão?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar a altura acima da parte inferior do recipiente que as massas antigirão após a colisão dos blocos.
Nós sabemos que as massas são idênticas, então cada objeto tem massa . E que essas massas colidem em um recipiente esférico de raio , ficando coladinhas após a colisão. Então, após a colisão a massa total passa a ser a soma das duas e a velocidade é a mesma.
Vamos aplicar a conservação de energia ao movimento para encontrar a velocidade antes e depois da colisão e aplicar a conservação de energia-impulso para a colisão.
Seja a velocidade da massa liberada no aro imediatamente antes de atingir a segunda massa.
Vamos lá!
Passo 2
A conservação de energia nos diz que:
Onde temos a energia cinética do lado esquerdo da equação e a energia potencial do lado direito. Sendo e o raio da trajetória.
Simplificando as massas:
Isolando nessa equação, vamos ter:
Esta é a velocidade para a colisão.
Passo 3
Seja a velocidade do objeto combinado logo após a colisão.
A conservação do momento aplicado à colisão dá:
Então, simplificando as massas e isolando na equação, temos:
Mas . Assim, substituindo, vamos ter:
Passo 4
Aplicando, agora, a conservação de energia ao movimento do objeto combinado após a colisão.
Seja a altura final acima do fundo do recipiente. Assim, considerando energia cinética antes e potencial depois, temos:
Isolando a altura na equação, teremos:
Substituindo :
Logo,
Valeu, galera! Até a próxima! 😉