Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 68

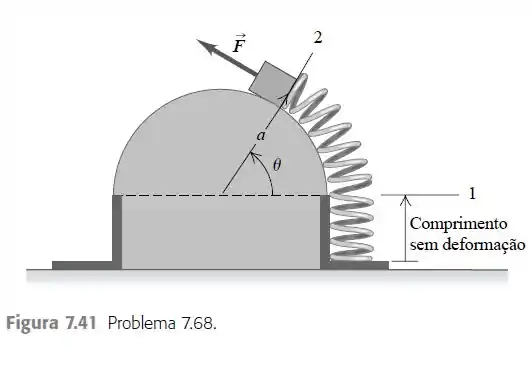
Uma força variável F → é mantida tangencialmente a uma superfície semicircular (Figura 7.41). Variando lentamente a força, um bloco de peso w estica a mola ao qual ele está preso da

posição 1 à posição 2. A massa da mola é desprezível e a constante da mola é k. A extremidade da mola percorre um arco de raio a. Calcule o trabalho realizado pela força F → .

Passo 1

Vamos aplicar a equação:

K 1 + U 1 + W o u t r a = K 2 + U 2

W o u t r a é o trabalho feito por F .

Temos que:

W o u t r a = ∆ K + ∆ U

A distância que a mola se estende é a θ .

E que:

y 2 - y 1 = a sen ⁡ θ

Passo 2

A força aumenta tanto a energia potencial gravitacional do bloco quanto a energia potencial da mola. Se o bloco é movido lentamente, a energia cinética pode ser tomada como constante; portanto, o trabalho realizado pela força é o aumento da energia potencial,

∆ U = m g a sen ⁡ θ + 1 2 k a θ 2

Passo 3

A força é mantida tangente à superfície para que o bloco fique em contato com a superfície.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A única força que age sobre uma partícula é a força conservativa F . Se a partícula está no ponto A , a energia potencial do sistema associada aF e à partícula é 40J . Se a partícula se move do pontoA
Uma força conservativa F ( x ) age sobre uma partícula de 2,0k g que se move ao longo de um eixo x . A energia potencial U ( x ) associada a F ( x ) está plotada na Fig. 8-61. Quando a partícula se en
Uma pedra de 0,050 kg se move dá origem ao ponto(3,0 m, 5,0 m) em um sistema de coordenadas no qual o sentido positivo do eixo Oy é de baixo para cima. a) A pedra inicialmente se move horizontalmente
Um homem com massa igual a 70,0 kg está sentado sobre uma plataforma suspensa por uma roldana conforme indicado na Figura 7.23 e se eleva com velocidade constante exercendo umaforça na corda que passa
Uma esquiadora de 60,0 kg parte do repouso no topo de uma pista de esqui inclinada com uma altura de 65,0 m .a ) Supondo que as forças de atrito realizam um trabalho total de - 10,5 kJ enquanto ela de