Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 15.1 - Ex. 22
A Figura 15-30 mostra um pulso no tempo movendo-se para a direta. (a) Neste instante, quais são os segmentos da corda que estão se movendo para cima? (b) Quais são os segmetos que estão se movendo para baixo? (c) Existe algum segmento da corda, no pulso, instantaneamente em repouso? Responda a estas questões fazendo um esboço do pulso em um tempo ligeiramente posterior e em um tempo ligeiramente anterior, para ver como os segmentos da corda estão se movendo.
Passo 1
Vamos fazer uma ilustração dos momentos antes e depois para ver como a onda está se comportando. Se liga só:
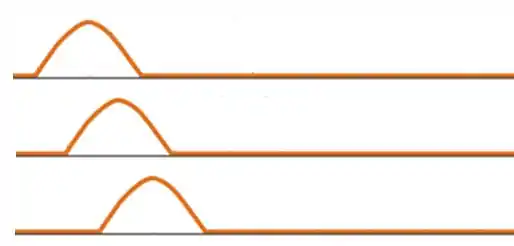
Perceba portanto, que o lado esquerdo do pulso está descendo a medida que o pulso se locomove e que o lado direito do pulso está subindo a medida que o pulso se locomove!
Passo 2
(a) Olhando a ilustração acima, podemos ver que o pedaço entre e , isso é, o lado direito do pulso, estão se movendo para cima.
(b) Agora queremos saber se tem algum pedaço se movendo para baixo. Vendo a ilustração, é possível concluir que os pontos entre 1 e 2, isso é, o lado esquerdo do pulso, estão indo para baixo.
Passo 3
(c) Nesse ultimo item queremos achar algum ponto em repouso, nesse caso é interessante procurarmos ponto de inflexões. Olha só para o ponto , viu que ele permanece em repouso?!
Resposta
- O segmento entre e 3
- O segmento entre e 2
- O ponto