Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 23

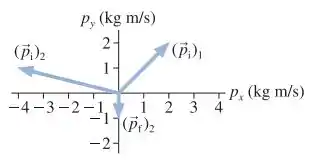
Duas partículas colidem uma com a outra e ricocheteiam. A figura EX9.23 mostra os momenta de ambos e o momentum final da partícula 2. Qual é o momentum final da partícula 1? Expresse sua resposta na forma de componentes.

Passo 1

O princípio da conservação da quantidade de movimento nos diz que a soma vetorial da quantidade de movimento deve permanecer constante antes e após a colisão.

Note que usamos a palavra “vetorial”. Isso quer dizer que a quantidade de movimento em x e em y devem ser conservadas.

Passo 2

Sendo assim, vamos começar calculando a quantidade de movimento inicial em x:

p i x = p i 1 x + p i 2 x

p i x = + 2   k g   m ⋅ s - 1 + - 4   k g   m ⋅ s - 1 = - 2   k g   m ⋅ s - 1

Agora, vamos calcular a quantidade de movimento final em x:

p f x = p f 1 x + p f 2 x = p f 1 x + 0

Como a quantidade de movimento deve ser conservada em x:

p i x = p f x ∴ - 2   k g   m ⋅ s - 1 = p f 1 x

⟹ p f 1 x = - 2   k g   m ⋅ s - 1

Passo 3

Agora, vamos fazer a mesma coisa para o eixo y:

p i y = p i 1 y + p i 2 y

p i y = + 2   k g   m ⋅ s - 1 + + 1   k g   m ⋅ s - 1 = 3   k g   m ⋅ s - 1

A quantidade de movimento final em y será:

p f y = p f 1 y + p f 2 y

p f y = p f 1 y + - 1   k g   m ⋅ s - 1

Como a quantidade de movimento deve ser conservada em y:

p i y = p f y ∴ 3 = p f 1 y + - 1   k g   m ⋅ s - 1

⟹ p f 1 y = 4   k g   m ⋅ s - 1

Resposta

Temos p → f 1 = - 2   k g   m ⋅ s - 1 i ^ + 4   k g   m ⋅ s - 1   j ^ .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Por que a seguinte situação é impossível? Um astronauta, junto com o equipamento que carrega, tem uma massa de 150k g . Ele está fazendo um passeio pelo espaço fora da nave, que está à deriva no espaç
Um corpo de massa m é atirado do solo com velocidade inicial v o , fazendo um ângulo θ com a horizontal. Mostre que a variação do momento linear do corpo até o instante em que ele atinge novamente o s
3 . Os objetos A, B e C estão se movendo conforme mostra a Figura E8.3. Ache os componentes x e y do momento linear resultante das partículas se definirmos que o sistema consiste em ( a ) A e C, ( b )
Momento linear e o peixe-arqueiro. Peixes-arqueiros são peixes tropicais que caçam atirando gotas d’água de suas bocas em insetos acima da superfície da água para jogá-los na água, onde o peixe pode c
Qual é a velocidade do peixe-arqueiro imediatamente depois de expelir a gota d’água? (a) 0,0025 m/s; (b) 0,012 m/s; (c) 0,75 m/s; (d) 2,5 m/s.