Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 56

Demonstre as Equações 8.4   para a aceleração de um projétil sujeito a uma força de arraste.

Passo 1

Olá, tudo bem?

Considerando um projétil, temos a força gravitacional (em azul) que é vertical para baixo e temos também uma força de arraste (em vermelho) que faz um ângulo θ com o eixo horizontal da seguinte forma:

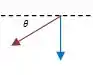
Segundo o capítulo 6 , a força de arraste tem a seguinte forma:

D → = 1 4 A v 2

A ideia aqui é aplicar a segunda lei de Newton tanto na direção horizontal, quanto na vertical.

Passo 2

Na vertical temos:

- m g - D s e n θ = m a y

a y = - g - D m s e n θ

a y = - A v 2 s e n θ 4 m - g

E na horizontal:

- D c o s θ = m a x

a x = - D m c o s θ = - A v 2 c o s θ 4 m

Passo 3

Agora precisamos lembrar que as componentes verticais e horizontais da velocidade podem ser dadas em função do módulo v e do ângulo θ :

v x = v c o s θ

v y = v s e n θ

E o módulo da velocidade em termos das componentes é:

v = v x 2 + v y 2

Então os termos v 2 s e n θ e v 2 c o s θ podem ser substituídos por:

v 2 s e n θ = v . v s e n θ = v x 2 + v y 2 . v y

v 2 c o s θ = v . v c o s θ = v x 2 + v y 2 . v x

E as componentes da aceleração ficam assim:

a x = - A v 2 c o s θ 4 m = - A v x v x 2 + v y 2 4 m a y = - A v y v x 2 + v y 2 4 m - g

Beleza?

Espero ter ajudado!

Vamos pra próxima?

Resposta

a x = - A v 2 c o s θ 4 m = - A v x v x 2 + v y 2 4 m a y = - A v y v x 2 + v y 2 4 m - g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os cavaleiros do rei Artur disparam um canhão do topo da muralha de um castelo. A bala de canhão é disparada com 50 m/s em um ângulo de 30º. Outra bala de canhão, que foi acidentalmente deixada cair,
Os navios A e B deixam o porto simultaneamente. Nas próximas duas horas, o navio A navega a 20 mph para 30° a oeste do norte, enquanto o navio B navega para 20° a leste do norte a 25 mph.Qual é a dist
Mike arremessa uma bola para cima e para leste em um ângulo de 63° com uma rapidez de 22 m/s. Nancy dirige seu carro para leste e passa por Mike a 30 m/s no exato instante em que este arremessa a bola
Um avião desenvolve uma velocidade relativa ao ar de 200 mph. O piloto deseja chegar a um destino 600 mi a leste, porém existe um vento soprando a 50 mph com orientação de 30° nordeste.a. Em que orien
Enquanto dirige seu carro para o norte, a 25 m/s, durante uma tempestade, você nota que as gotas caem formando um ângulo de 38° com a vertical. Ao dirigir de volta para casa, momentos mais tarde, com