Duas partículas puntiformes positivas iguais, , estão no eixo em e . (a) Obtenha uma expressão para o campo elétrico no eixo como função de . (b) Uma partícula de massa e carga move-se ao longo do eixo em um fio estivado sem atrito. Determine a força elétrica exercida na partícula em função de e determine o sinal de tal que esta força sempre aponte no sentido que se afaste da origem. (c) A partícula está inicialmente em repouso na origem. Se ela receber um pequeno cutucão na direção , qual a rapidez da partícula no instante que a força resultante sobre ela for máxima? (Despreze quaisquer efeitos devidos à gravidade).
Passo 1
- Veja o esquema a seguir:
- Temos que
- Usando o teorema da energia cinética, temos que
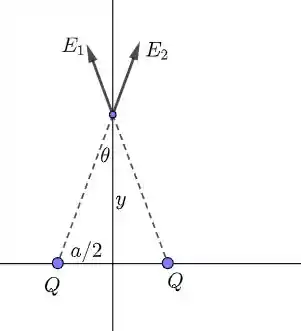
Temos que
Assim, o campo resultante será:
Passo 2
Para que essa força sempre aponte para a origem, essa carga deve ser negativa (pois a força apontará no sentido contrário ao do campo).
Passo 3
onde o trabalho é o trabalho da força . Temos:
Fazendo , temos que , de forma que
Precisamos encontrar . Notemos que a força será máxima quando . Assim,
ou seja,
Passo 2
Assim, segue que:
Ou seja,