Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 30

O eixo de um recipiente cilíndrico é vertical. O recipiente é preenchido com massas iguais de água e óleo. O óleo flutua em cima da água, e a superfície livre do óleo está a uma altura h acima da base do recipiente. Qual é a altura h, se a pressão no fundo da água é 10 kPa maior do que a pressão na superfície do óleo? Suponha a massa específica do óleo igual a 875 kg/m³.

Passo 1

Para que a gente consiga visualizar melhor o que o problema está nos pedindo temos que desenhar a situação.

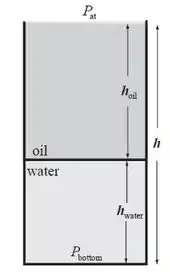
O óleo está na parte superior e existe sobre ele somente a pressão atmosférica. O que nós queremos achar aqui é a altura h, ou seja:

h = h á g u a + h ó l e o

Bom, nós sabemos que as massas são iguais:

m á g u a = m ó l e o

Agora temos que lembrar que pela fórmula da massa específica temos:

m = ρ V

Sabemos que V = A . h :

m = ρ A . h

Substituindo na equação das massas:

ρ á g u a . A . h á g u a = ρ ó l e o A . h ó l e o

A área será igual para as duas:

ρ á g u a . h á g u a = ρ ó l e o . h ó l e o

Achamos uma relação entre as alturas, mas ainda não conseguimos resolver a questão!

Passo 2

Bom, precisamos achar mais uma relação entre as alturas para conseguir resolver o problema. E para isso podemos usar a equação da pressão:

P = F A

Como nós temos uma variação na pressão:

∆ P = F A

A força que está presente neste sistema é causada somente pela força peso exercida sobre a coluna de fluido, ou seja:

∆ P = m á g u a . g + m ó l e o . g A

Já sabemos como calcular a massa:

∆ P = g . ρ á g u a . A . h á g u a + ρ ó l e o A . h ó l e o A

∆ P g = ρ á g u a . h á g u a + ρ ó l e o . h ó l e o

Sabemos do Passo 1 que:

ρ á g u a . h á g u a = ρ ó l e o . h ó l e o

Substituímos:

∆ P g = ρ á g u a . h á g u a + ρ á g u a . h á g u a = 2 ρ á g u a . h á g u a

Já sabemos que:

∆ P = 10   k P a

g = 9,81   m / s ²

ρ a g u a = 1000   k g / m ³

Agora sim! É só colocar estes dados na fórmula para achar a altura da água:

10   k P a 9,81   m / s ² = 2 . 1000   k g / m 3 . h á g u a

h á g u a = 0,51   m

A mesma relação vale para o óleo:

∆ P g = 2 ρ ó l e o . h ó l e o

Sabendo que:

ρ ó l e o = 875   k g / m ³

10   k P a 9,81   m / s ² = 2 . 875   k g / m 3 . h ó l e o

h ó l e o = 0,58   m

Estamos quase lá! Se queremos h, basta substituirmos estes valores na primeira equação que conseguimos:

h = 0,51   m + 0,58   m = 1,1   m

Resposta

h = 1,1   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o aumento de pressão do fluido em uma seringa quando uma enfermeira aplica uma força de 42N ao êmbolo circular da seringa, que tem um raio de 1,1c m .
Um peixe se mantém na mesma profundidade na água doce ajustando a quantidade de ar em ossos porosos ou em bolsas de ar para tornar sua massa específica média igual à da água. Suponha que, com as bolsa
Quando uma corrente de água sai suavemente de uma torneira, sua largura diminui à medida que a água cai. Explique por que isso acontece.
(a) Calcule a diferença na pressão sanguínea entre os pés e o topo da cabeça de uma pessoa de 1,65 m de altura. (b) Considere um segmento cilíndrico de um vaso sanguíneo de 2,0 cm de comprimento e 1,5
Em uma demonstração, uma professora separa facilmente dois hemisférios ocos de aço (diâmetro D) por meio de uma alça presa a cada um deles. A seguir, ela os encaixa novamente, bombeia o ar para fora d