Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 83

Uma casca esférica de cobre, com um diâmetro externo de 12,0   c m , flutua na água com metade do seu volume acima da superfície da água. Determine o diâmetro interno da casca. A cavidade dentro da casca esférica está vazia.

Passo 1

Opa, e aí, tudo firmeza? Espero que sim, bora solucionar mais uma questão? Queremos o diâmetro interno d i n de uma casca esférica, sendo que a gente tem o diâmetro externo d o u t = 0,12   m . Como ela está flutuando, podemos aplicar o equilíbrio de forças nessa casca

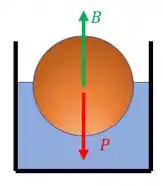
Já que a casca está paradinha, podemos dizer que

P = B

Temos a força peso P = m g e a força devido ao empuxo B :

m g = B

A fórmula do empuxo causado pelo deslocamento de água é

B = ρ H 2 O ∙ V H 2 O D e s l o c a d a ∙ g

Substituindo isso na nossa equação de equilíbrio

m g = ρ H 2 O ∙ V H 2 O D e s l o c a d a ∙ g

m = ρ H 2 O ∙ V H 2 O D e s l o c a d a

Aí nós vamos usar essa equação para achar o d i n . Vem ver como fica!

Passo 2

O volume de água deslocado é o volume da casca que está submerso.

V H 2 O D e s l o c a d a = V '

O enunciado diz que metade da casca esférica está submersa. Sendo que ela é oca, então o volume submerso V ' da casca esférica é a metade do volume de uma esfera de diâmetro d o u t .

O volume de uma esfera é

V e s f e r a = 4 π 3 r 3

Se formos usar o diâmetro

r = d o u t 2

V e s f e r a = 4 π 3 d o u t 2 3 = 4 π 3 d o u t 3 8

Mas lembra que V ' é metade disso

V e s f e r a = 1 2 4 π 3 d o u t 3 8

V ' = π 12 d o u t 3

Podemos também expressar m em termos de d i n e d o u t . Temos que

ρ c o b r e = m V c a s c a

m = ρ c o b r e V c a s c a

O volume da casca vai ser o volume de uma esfera de diâmetro d o u t menos o volume de uma esfera de diâmetro d i n :

m = ρ c o b r e 4 π 3 d o u t 3 - d i n 3 8  

m = ρ c o b r e π 6 d o u t 3 - d i n 3

Obs: repara que ao ver o volume de água deslocado, achamos o volume que a casca ocupa no espaço, contando com o seu interior. Já ao calcular a massa da casca, calculamos seu volume, considerando o diâmetro interno.

Passo 3

Vamos substituir o que a gente achou na nossa equação de equilíbrio

m = ρ H 2 O ∙ V H 2 O D e s l o c a d a

ρ c o b r e π 6 d o u t 3 - d i n 3 = ρ H 2 O ∙ π 12 d o u t 3

ρ c o b r e d o u t 3 - d i n 3 = ρ H 2 O ∙ d o u t 3 2

Isolando d i n :

ρ c o b r e d o u t 3 - ρ c o b r e d i n 3 = ρ H 2 O ∙ d o u t 3 2

ρ c o b r e d o u t 3 - ρ H 2 O ∙ d o u t 3 2 = ρ c o b r e d i n 3

d i n = ρ c o b r e d o u t 3 - ρ H 2 O ∙ d o u t 3 2 ρ c o b r e 3

Nós achamos as massas específicas da água e do cobre na tabela 13-1:

ρ H 2 O = 10 3 k g m 3

ρ H 2 O = 8,93 × 10 3 k g m 3

Substituindo isso e o diâmetro externo d o u t = 0,12   m :

d i n = 8,93 × 10 3 0,12 3 - 10 3 ∙ 0,12 3 2 8,93 × 10 3 3

d i n = 0 , 118   m

d i n = 11,8   c m

Resposta

d i n = 11.8   c m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cubo de isopor, 25c m em uma borda, é colocado em uma panela de uma balança. A balança está em equilíbrio quando uma massa de 20g de latão é colocada na outra panela. Encontre a massa do cubo de is
Dois corpos diferem em massa específica e em massa. O corpo A tem uma massa que é oito vezes a massa do corpo B. A massa específica do corpo A é quatro vezes a massa específica do corpo B. Como os vol
Dois corpos esféricos diferem em tamanho e massa. O corpo A tem uma massa que é oito vezes a massa do corpo B. O raio do corpo A é o dobro do raio do corpo B. Como suas massas específicas se comparam?
Uma esfera é construída colando-se dois hemisférios. A massa específica de cada hemisfério é uniforme, mas a massa específica de uma deles é maior do que a massa específica do outro. Verdadeiro ou Fal
Uma bola de 50,0 g consiste em uma casca esférica plástica com o interior cheio de água. A casca tem um diâmetro externo de 50,0 mm e um diâmetro interno de 20,0 mm. Qual é a massa específica do plást