Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.10 - Ex. 37

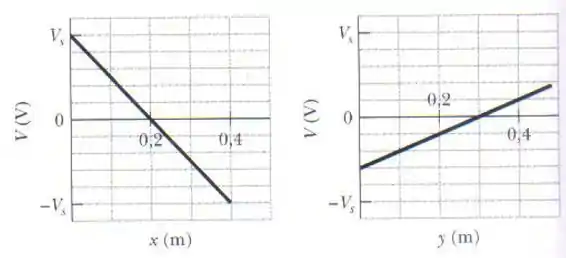
Um elétron é colocado no plano xy, onde o potencial elétrico varia com x e y de acordo com os gráficos da figura abaixo (o potencial não depende de z) . Em termos dos vetores unitários, qual é a força a que é submetido o elétron? A escala do eixo vertical é definida por .

Passo 1

Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui o que temos é uma situação onde um elétron se movimenta em uma regial de potencial elétrico variável, e consequentemente ele é submetido a uma força. O que iremos fazer aqui é descobrir qual é a força que ele é submetido.

Lembra que o campo elétrico é menos o gradiente do potencial?

E que o valor campo em cada direção é menos a derivada parcial naquela direção?

Derivadas parciais são derivadas. E derivadas são inclinações de retas tangentes. Então para achar e queremos achar as inclinações das tangentes. Que tangentes? As tangentes aos gráficos de e . Só que o gráfico de e são retas. Então a inclinação das retas tangentes (as derivadas) são a inclinação da própria reta do gráfico.