Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 28.Problemas Adicionais - Ex. 68b
Um elétron do tubo de imagem de um receptor de televisão antigo está se movendo a na presença de um campo magnético de . Determine (b) o valor mínimo da força que o campo magnético pode exercer sobre o elétron.
Passo 1
A gente tira lá da teoria a seguinte expressão para a força exercida por um campo magnético e a velocidade da partícula.
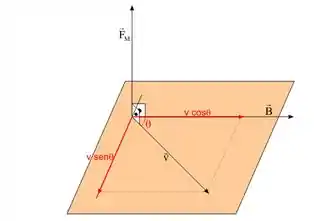
A partir dela, podemos inferir as seguintes situações:
- Se , então ;
- Se , então , portanto ;
- Se , então , portanto .
Passo 2
Assim, vamos calcular a força mínima! Ela será minima quando a velocidade é paralela ao campo, ou seja, .
Resposta
A força mínima é
Exercícios de Livros Relacionados
Uma certa partícula subatômica decai em um elétron e um pósitron. Suponha que, no instante do decaimento, a partícula está em repouso em um campo magnético uniforme B → de módulo 3,53 m T e que as tra
Uma partícula penetra em uma região onde existe um campo magnético uniforme, com o vetor velocidade da partícula perpendicular à direção do campo. A Fig. 28-36 mostra o período T do movimento da partí
Qual é o valor do campo magnético uniforme, aplicado perpendicularmente a um feixe de elétrons que se movem com uma velocidade de 1,30 × 10 6 m / s , que faz com que a trajetória dos elétrons seja um
Uma fonte injeta um elétron de velocidade v = 1,5 × 10 7 m / s em uma região onde existe um campo magnético uniforme de módulo B = 1,0 × 10 - 3 T . A velocidade do elétron faz um ângulo 10 º º com a d
Um elétron é acelerado a partir do repouso por uma diferença de potencial de 350 V. Em seguida, o elétron entra em uma região onde existe um campo magnético uniforme de módulo 200 mT com uma velocidad