Encontre o centro de massa da folha uniforme de madeira na figura. Considere esse sistema como efetivamente composto de duas folhas, supondo que uma “massa negativa” para compensar o buraco. Portanto, uma é um quadrado de de lado e massa e a segunda é uma folha retangular com uma massa . Tome a origem do sistema de coordenadas no canto inferior esquerdo da folha.
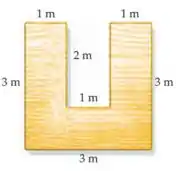
Passo 1
Vamos desenhar o nosso sistema de coordenadas na figura:
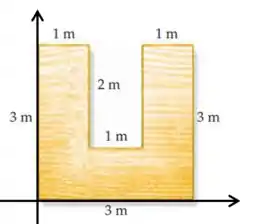
E seguindo a orientação do enunciado, vamos primeiro procurar o centro de massa de um quadrado de lado :
Passo 2
E agora vamos considerar o de um retângulo de lados .Vamos usar outro sistema de coordenadas para facilitar a conta:
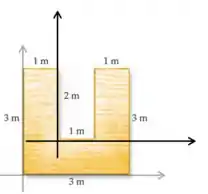
E então:
E agora é só “converter” essas coordenadas para o sistema antigo.
Para ir de um sistema a outro, nós simplesmente andamos metro para a direita no eixo e metro para cima no eixo . Então, no sistema antigo, as coordenadas do centro de massa do retângulo são:
Passo 3
Agora sim, é só fazer a média ponderada desses dois pontos, considerando que o retângulo tem massa “negativa”:
E agora só precisamos de expressões para e . Se a densidade superficial da placa é dada por , podemos usar a seguinte relação:
Onde é a área de cada placa:
E então:
Resposta
O centro de massa da folha está localizado em .