Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 104
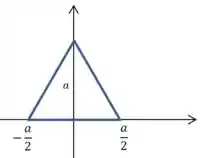
Por simetria, localize o centro de massa de uma folha uniforme em forma de triângulo equilátero com lados de comprimento . O triângulo tem um vértice no eixo e os outros em e .
Passo 1
Qual será a coordenada do centro de massa? Bom, o triângulo é totalmente simétrico em relação ao eixo , então:
Passo 2
Agora vamos explorar o fato de que o triângulo é equilátero. As bissetrizes formam ângulos de e dividem o lado oposto na metade:
O ponto onde essas bissetrizes se intersectam definem o “centroide” de um triângulo equilátero. Como nosso triângulo é homogêneo, esse também será o centro de massa.
Então é altura daquele ponto vermelho:
Então as coordenadas do centro de massa são:
Resposta
A posição do centro de massa é .
Exercícios de Livros Relacionados
A Fig. 9-35 mostra um sistema de três partículas de massas m 1 = 3,0k g , m 2 = 4,0k g e m 3 = 8,0k g . As escalas do gráfico são definidas por x s = 2,0m e y s = 2,0m . Quais são (a) a coordenada x e
(a) A que distância do centro da Terra se encontra o centro de massa do sistema Terra- Lua? (O Apêndice C fornece as massas da Terra e da Lua e a distância entre os dois astros .) (b) A que porcentage
O roteiro de um filme de ação requer que um pequeno carro de corrida (com uma massa de 1500k g e um comprimento de 3,0m ) acelere ao longo de uma barcaça ( com uma massa de 4000k g e um comprimento de
A Fig. 9-82 mostra uma placa quadrada uniforme de lado 6 d=6,0m da qual um pedaço quadrado de lado 2 d foi retirado. Quais são (a) a coordenadax e (b) a coordenada y do centro demassa da parte restant
Três massas pontuais de 2,0k g cada estão localizadas sobre o eixo x . Uma está sobre a origem, outra em x = 0,20m e outra em x = 0,50m . Encontre o centro de massa do sistema.