Enunciado
Física - Tipler - Vol 3- Ed: 6º - Capítulo 34.1 - Ex. 41
Encontre a energia do estado fundamental (n = 1) e dos dois primeiros estados excitados de um nêutron em uma caixa unidimensional de comprimento L = 1,00 × 10–15 m = 1,00 fm (aproximadamente o diâmetro de um núcleo atômico). Faça um diagrama de nível de energia para este sistema. Calcule o comprimento de onda da radiação eletromagnética emitida quando o nêutron faz uma transição de (b) n = 2 para n = 1, (c) n = 3 para n = 2 e (d) n = 3 para n = 1.
Passo 1
(a) Podemos achar a energia do estado fundamental pela equação:
Primeiro, passando para elétron-volt:
Assim, para um nêutron numa caixa de comprimento :
Para os outros estados, vamos usar a relação:
Assim, para :
E para :
Passo 2
Para montar o diagrama, vamos usar essa relação entre as energias nos estados excitados com a energia no estado fundamental:
Assim, cada nível será vezes maior que o estado fundamental:
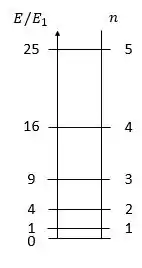
Passo 3
(b) O comprimento de onda da radiação eletromagnética emitida quando o nêutron transita de um estado para outro é dado pela equação de Einstein para energia de fótons:
Então, de :
Dessa forma:
Passo 4
(c) De :
Dessa forma:
Passo 5
(d) De :
Dessa forma:
Resposta
(a) ; ;
(b)
(c)
(d)